Table of Contents
Đối với các bạn học sinh có lẽ không còn xa lạ với hình thang. Đây là dạng hình rất hay được sử dụng trong các bài tập hình học, đặc biệt là những bài toán nâng cao. Bài viết này sẽ tổng hợp tất cả các kiến thức liên quan đến tính chất hình thang, hãy cùng ôn lại ngay nhé!
1. Hình thang
Hình thang là một tứ giác lồi có 2 cạnh đối song song. Hai cạnh này được gọi là hai cạnh đáy của hình thang. Hai cạnh còn lại là hai cạnh bên,
Các trường hợp đặc biệt của hình thang:
- Hình thang vuông: Hình thang có 1 góc vuông được gọi là hình thang vuông
- Hình thang cân: Hình thang có 2 góc kề một cạnh đáy bằng nhau là hình thang cân.
- Hình thang vuông cân: Là hình thang vừa vuông vừa cân và còn được gọi là hình chữ nhật.
» Xem thêm: Hình thang là gì? Các trường hợp đặc biệt của hình thang
2. Các tính chất của hình thang
2.1. Tính chất về góc
- Hai góc kề một cạnh bên của hình thang có tổng bằng 180 độ (nằm ở vị trí trong cùng phía của hai đoạn thẳng song song là 2 cạnh đáy).
- Đối với hình thang cân thì hai góc kề một cạnh đáy bằng nhau.
2.2. Tính chất về cạnh
- Hình thang có 2 cạnh đáy bằng nhau thì hai cạnh bên sẽ song song và bằng nhau.
- Ngược lại, nếu hình thang có 2 cạnh bên song song thì chúng sẽ bằng nhau và 2 cạnh đáy bằng nhau.
- Hình thang cân có 2 đường chéo bằng nhau.
2.3. Tính chất về đường trung bình
Đường trung bình là đường thẳng nối trung điểm hai cạnh bên của hình thang.
- Tính chất 1: Đường thẳng đi qua trung điểm 1 cạnh bên của hình thang và song song với 2 cạnh đáy thì sẽ đi qua trung điểm của cạnh bên còn lại.
- Tính chất 2: Đường trung bình của hình thang sẽ song song với 2 cạnh đáy và bằng ½ tổng 2 đáy.
2.4. Công thức tính diện tích hình thang
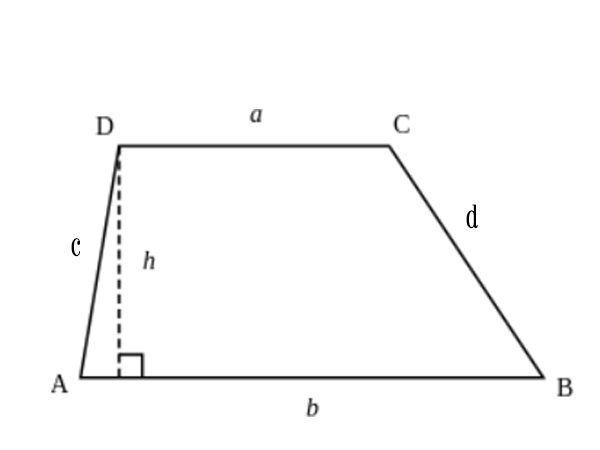
Hình minh họa (Nguồn: Internet)
Diện tích hình thang bằng chiều cao nhân với ½ tổng 2 đáy.
2.5. Công thức tính chu vi hình thang
Chu vi hình thang bằng tổng độ dài 2 đáy và 2 cạnh bên.
P = a + b + c + d
3. Các dạng bài thông dụng về tính chất hình thang
Bài tập 1: Cho hình thang ABCD (AB//CD), biết
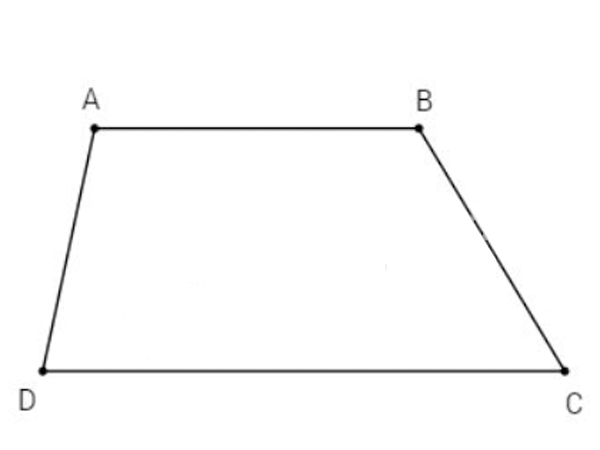
Hình minh họa (Nguồn: Internet)
Bài giải:
Bài tập 2: Cho hình thang ABCD có đáy lớn AB. Gọi M, N, P, Q lần lượt là trung điểm của đoạn thẳng AD, BC, AC, BD. Yêu cầu:
- Chứng minh bốn điểm M, N, P, Q nằm trên cùng một đường thẳng.
- Cho AB = a, CD = b (với a > b). Tính độ dài các đoạn MN, PQ.
- Chứng minh nếu MP = PQ = QN thì a - 2b = 0
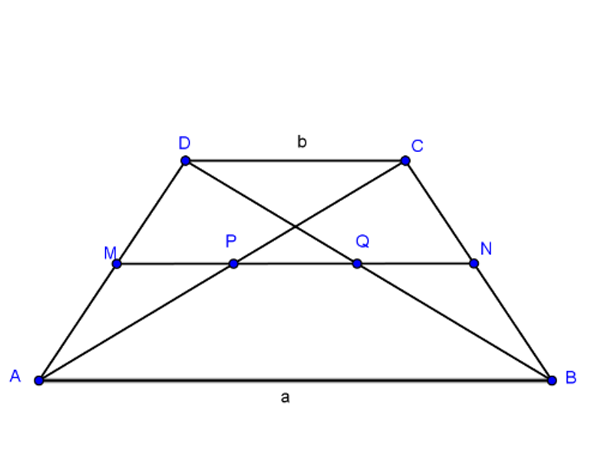
Hình minh họa (Nguồn: Internet)
Bài giải:
- Nhìn vào hình ta có thể dễ dàng thấy MP//DC và MQ//AB
Kết hợp với AB//DC suy ra MP 
MQ
=> Ba điểm M, P, Q thẳng hàng
Tương tự, 3 điểm N, P, Q thẳng hàng
Suy ra 4 điểm M, N, P, Q nằm trên cùng một đường thẳng.
- Ta có MN là đường trung bình của hình thang ABCD
Suy ra: MN = ½ (a+b)
Mặt khác ta có:
MQ = ½ AB =½ a;
MP = ½ DC = ½ b;
PQ = MQ - MP = ½ (a-b)
- Khi MP = PQ = QN => ⅓ MN = PQ
Suy ra ⅙ (a+b) = ½ (a-b)
=> (a+b) = 3(a-b) => a = 2b
Bài tập 3: Cho hình thang ABCD, đáy AB = 40 (đvđd), CD = 80 (đvđd), cạnh bên BC = 50 (đvđd) và AD = 30 (đvđd). Yêu cầu: Chứng minh ABCD là hình thang vuông.
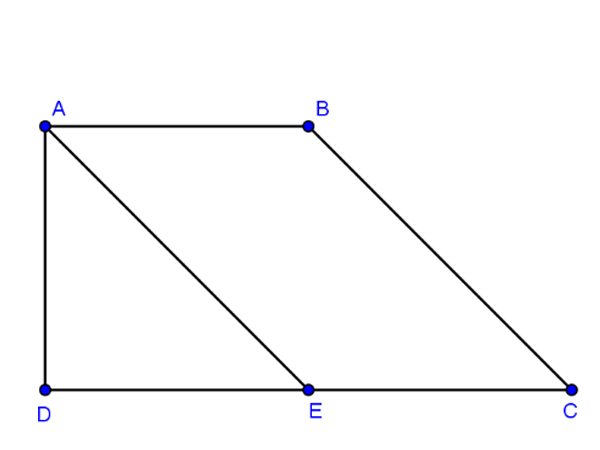
Hình minh họa (Nguồn: Internet)
Bài giải:
Từ đỉnh A kẻ đường thẳng song song với BC và cắt DC tại E.
Ta có: AE = BC = 50 (đvđd); EC = AB = 40 (đvđd)
=> DE = 80 - 40 = 40 (đvđd)
Tam giác ADE có AD = 30 (đvđd), DE = 40 (đvđd) và AE = 50 (đvđd)