Hai góc bù nhau là gì? Hai góc bù nhau bằng bao nhiêu độ?

Ở bài học trước chúng ta đã tìm hiểu về góc và cách vẽ góc khi biết trước số đo. Bài viết này sẽ giúp chúng ta tìm hiểu về mối liên hệ giữa các góc, cụ thể là hai góc bù nhau. Để có thể nắm vững bài học về hai góc bù nhau, cách vẽ hai góc bù nhau và phương pháp giải các bài tập liên quan đến hai góc bù nhau các bạn hãy theo dõi bài viết này nhé!

1. Hai góc bù nhau là gì? Hai góc bù nhau bằng bao nhiêu độ?

- Hai góc có tổng số đo 180° được gọi là hai góc bù nhau.

Ví dụ:

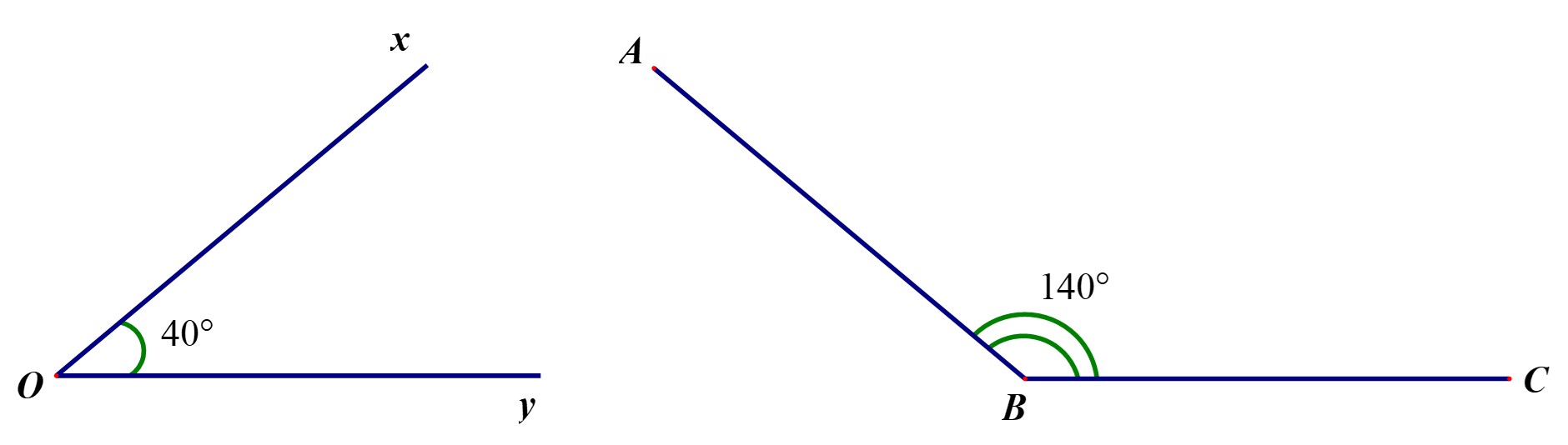
Ta có:

Nên là hai góc bù nhau.

2. Thế nào là hai góc kề bù?

Hai góc kề bù là hai góc vừa kề nhau, vừa bù nhau. Hay nói cách khác hai góc kề bù là hai góc có một cạnh chung còn hai cạnh còn lại nằm trên hai nửa mặt phẳng đối nhau có bờ là cạnh chung và tổng số đo hai góc bằng 180 độ.

Ví dụ:

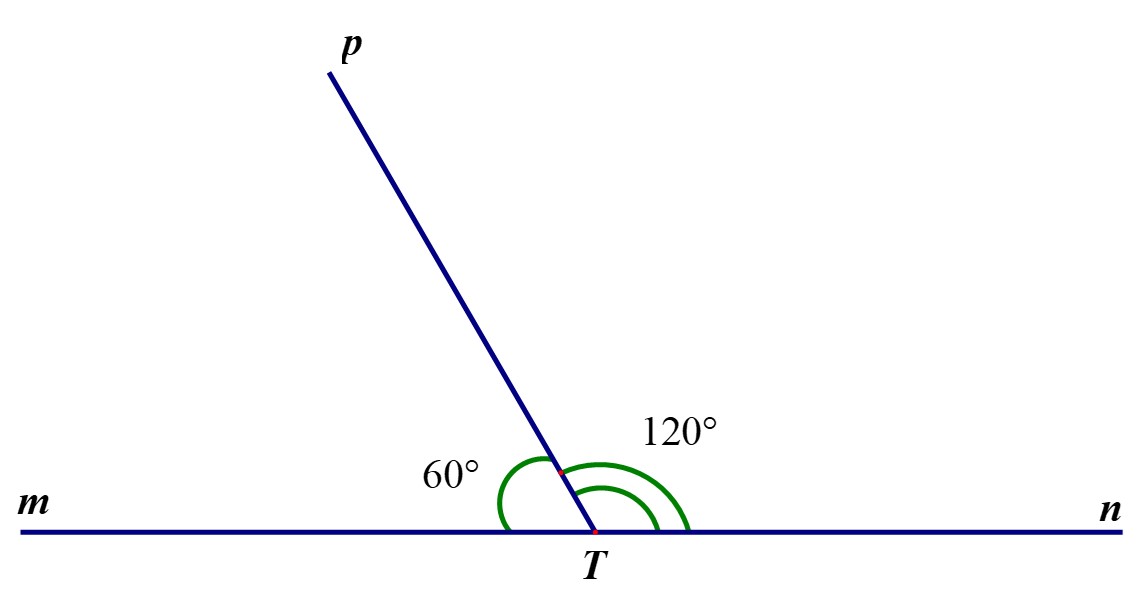
Dựa vào hình vẽ ta thấy là hai góc kề nhau và

nên là hai góc kề bù.

Ngoài ra ta có thể thấy hai góc có một cạnh chung là tia Tp và hai cạnh còn lại Tn, Tm là hai tia đối nhau.

» Xem thêm: Hai góc kề bù là gì? Cách làm các dạng bài tập liên quan

3. Tính chất hai góc bù nhau, hai góc kề bù

- Nếu là hai góc bù nhau thì .

- Nếu Ax và Ay là hai tia đối nhau, với tia Az bất kỳ khác tia Ax và Ay thì là hai góc kề bù. Khi đó, ta có: .

4. Các dạng toán liên quan hai góc bù nhau & hai góc kề bù

4.1. Dạng 1: Nhận biết hai góc bù nhau, hai góc kề bù, vẽ góc bù với góc đã cho hoặc kề bù với góc đã cho

*Phương pháp giải:

- Để nhận biết hai góc đã cho có phải là hai góc bù nhau không ta sẽ tính tổng của hai góc đó. Nếu tổng hai góc bằng 180° thì kết luận hai góc đã cho bù nhau. Ngược lại, nếu tổng hai góc không bằng 180° thì hai góc đã cho không phải là hai góc bù nhau. 

- Để vẽ góc bù với góc đã cho ta làm như sau:

• Bước 1: Tìm số đo góc bù với góc đã cho. Chúng ta đã biết hai góc bù nhau là hai góc có tổng số đo bằng 180°. Vì thế để tính góc còn lại ta lấy 180 độ trừ đi góc đã cho.
• Bước 2: Sau đó chúng ta áp dụng cách vẽ góc khi biết số đo góc để vẽ góc cần tìm.

- Để vẽ góc kề bù với góc đã cho ta làm như sau:

• Bước 1: Dựa vào yêu cầu của đề xác định cạnh chung của hai góc.
• Bước 2: Sau đó, chúng ta vẽ tia đối của cạnh còn lại. Khi đó góc tạo bởi cạnh chung và tia vừa vẽ chính là góc cần tìm.

- Vì hai góc kề bù có tổng số đo bằng 180° nên để tính góc kề bù với góc đã cho ta lấy 180° trừ đi góc đã cho.

Ví dụ 1. Các cặp góc sau đây có phải là hai góc bù nhau không?

a)

b)

c)

Giải.

a) Ta có: nên là hai góc bù nhau.

b) Ta có: nên là hai góc không bù nhau.

c) Ta có: nên là hai góc bù nhau.

Ví dụ 2. Vẽ và tính góc kề bù với các góc sau đây:

a) Góc kề bù với góc 

b) Góc kề bù với góc 

Giải.

a) Ta có hai góc có tia Ov là cạnh chung vì thế để vẽ góc kề bù với góc ta vẽ tia On là tia đối của tia Ou.

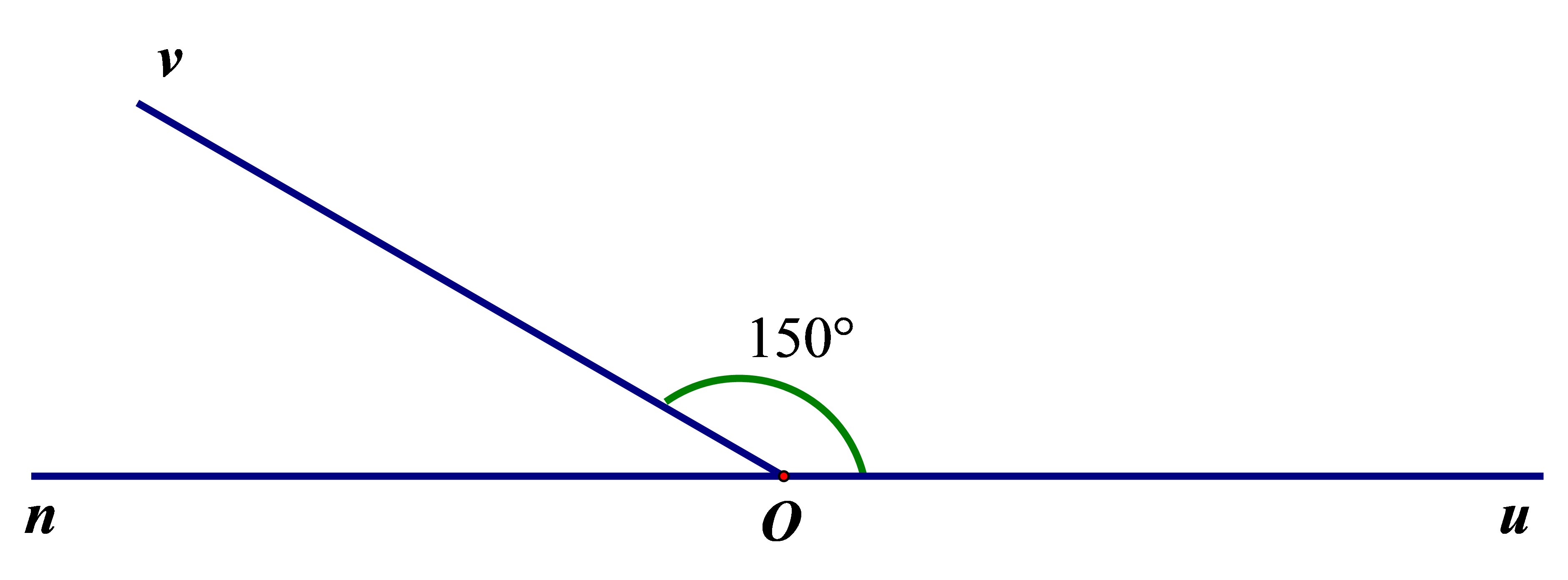
Ta có là hai góc kề bù nên 

b) Ta có hai góc có tia Cm là cạnh chung vì thế để vẽ góc kề bù với góc ta vẽ tia Cp là tia đối của tia Ou.

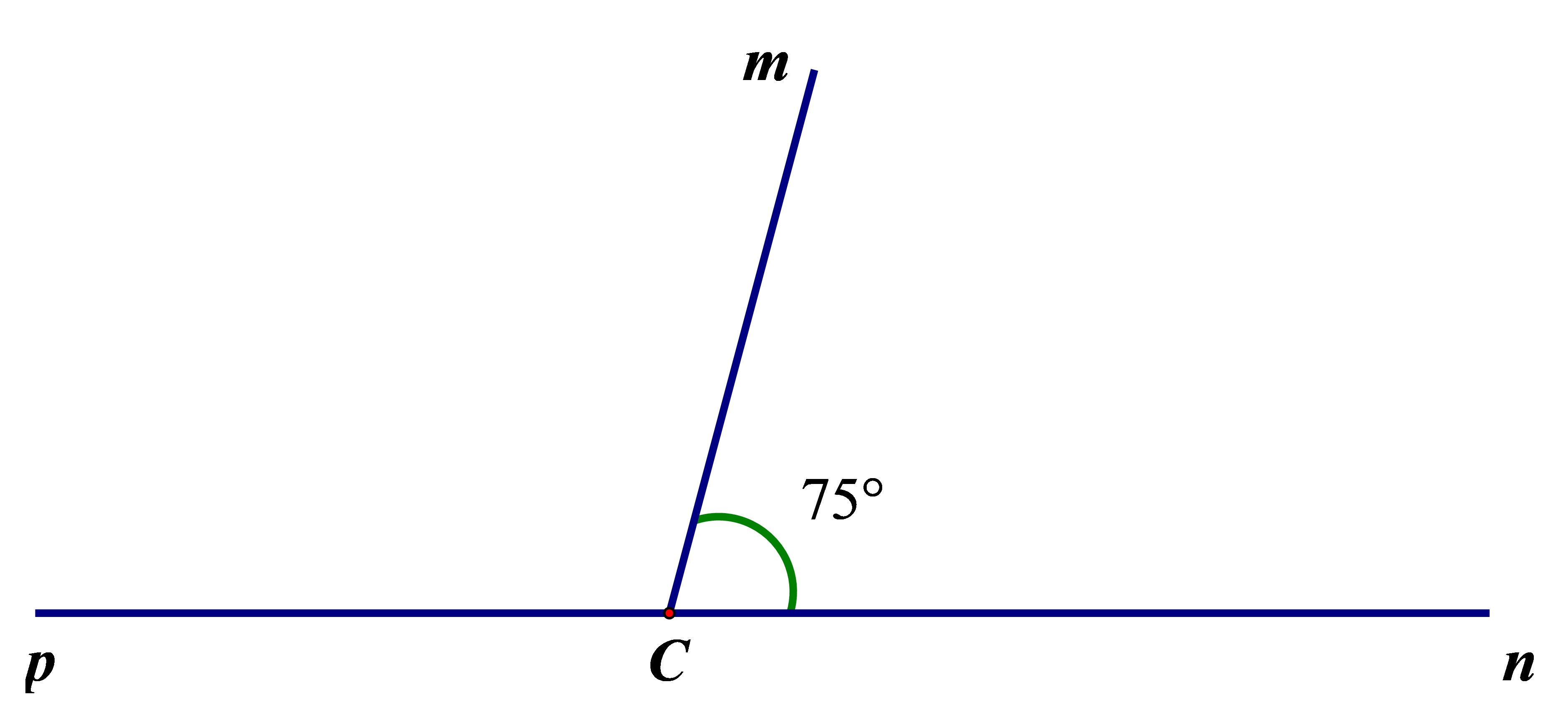
Ta có là hai góc kề bù nên

4.2. Dạng 2: Giải các bài tập tính toán liên quan đến hai góc bù nhau, hai góc kề bù.

*Phương pháp giải:

Phân tích yêu cầu bài toán, các giả thiết đề bài cho và áp dụng tính chất của hai góc bù nhau, hai góc kề bù để tìm cách giải bài toán.

Ví dụ 3. Cho là hai góc bù nhau, trong đó . Vẽ tia Az là tia đối của tia An. Tính góc .

Giải.

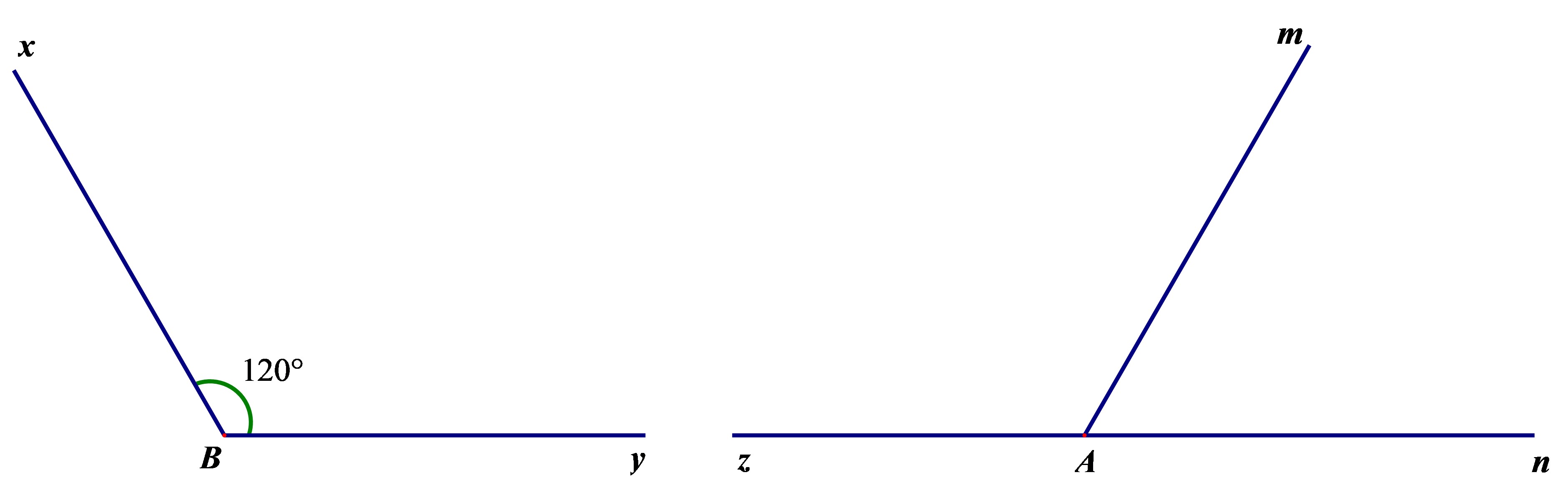
Ta có là hai góc bù nhau nên 

Vì tia Az là tia đối của tia An nên là hai góc kề bù.

Suy ra 

5. Các bài tập luyện tập vận dụng tính chất hai góc bù nhau, hai góc kề bù

Bài 1. Cho và tia Ou là tia đối của tia Ov. Khi đó hai góc được gọi là hai góc gì? Và góc bằng bao nhiêu độ?

A. là hai góc đối đỉnh và .

B. là hai phụ nhau và .

C. là hai góc nhọn và .

D. là hai góc kề bù và .

Bài 2. Cho , khi đó được gọi là hai góc:

A. Kề nhau

B. Kề bù

C. Bù nhau

D. Phụ nhau

Bài 3. Trong các cặp góc sau, cặp góc nào bù nhau?

A.

B.

C.

D.

Bài 4. Cho là hai góc bù nhau, trong đó . Vẽ tia Ox là tia đối của tia Op. So sánh hai góc và . Và rút ra nhận xét về hai góc cùng bù với một góc.

Như vậy, nội dung trên VOH Giáo Dục đã tổng hợp kiến thức để học sinh hiểu thế nào là hai góc bù nhau, hai góc kề bù; tính chất của hai góc bù nhau, hai góc kề bù và đưa ra phương pháp giải các dạng bài tập thường gặp. Hy vọng qua bài viết này sẽ giúp các bạn học sinh nắm vững kiến thức ở chuyên đề này từ đó các bạn có thể làm tốt các bài tập trên lớp.

Chịu trách nhiệm nội dung: GV Nguyễn Thị Trang