Table of Contents
Phương trình tiếp tuyến là một kiến thức quan trọng trong toán học lớp 11. Nó liên quan đến việc tìm phương trình của đường tiếp tuyến trên đồ thị của hàm số. Điều này giúp xác định độ dốc của đường cong tại một điểm và áp dụng trong các bài toán về đạo hàm và tốc độ thay đổi. Dưới đây là tổng hợp đầy đủ các kiến thức viết phương trình tiếp tuyến gồm khái niệm và 3 dạng bài toán thương gặp nhất VOH Giáo dục chia sẻ cho các em học sinh tham khảo:
1. Khái niệm phương trình tiếp tuyến
Tiếp tuyến của một đường cong tại một điểm bất kì thuộc đường cong là một đường thẳng chỉ "chạm" vào đường cong tại điểm đó. Tiếp tuyến như một đường thẳng nối một cặp điểm gần nhau vô hạn trên đường cong. Chính xác hơn, một đường thẳng là một tiếp tuyến của đường cong y = f (x) tại điểm x = c trên đường cong nếu đường thẳng đó đi qua điểm (c, f (c)) trên đường cong và có độ dốc f '(c) với f ' là đạo hàm của f.
Khi tiếp tuyến đi qua điểm giao của đường tiếp tuyến và đường cong trên, được gọi là tiếp điểm, đường tiếp tuyến "đi theo hướng" của đường cong, và do đó là đường thẳng xấp xỉ tốt nhất với đường cong tại điểm tiếp xúc đó.
Mặt phẳng tiếp tuyến của mặt cong tại một điểm nhất định là mặt phẳng "chỉ chạm vào" mặt cong tại điểm đó.
- Hệ số góc k của tiếp tuyến chính là f′(x) . Vậy khi bài toán cho hệ số góc k thì các bạn sẽ đi giải phương trình sau:
f′(x0) = k; với x0 là hoành độ tiếp điểm.
Giải phương trình này các bạn sẽ tìm được x0, từ đó sẽ tìm được y0 .
Đạo hàm của hàm số y = f(x) tại điểm x0 là hệ số góc của tiếp tuyến với đồ thị (C) của hàm số tai điểm M(x0;y0).
Khi đó phương trình tiếp tuyến của (C) tại điểm M(x0;y0) là y = y′(x0)(x−x0) + y0
Nguyên tắc chung để lập được phương trình tiếp tuyến ta phải tìm được hoành độ tiếp điểm x.
2. Các dạng toán thường gặp viết phương trình tiếp tuyến
- Viết phương trình tiếp tuyến tại tiếp điểm M
- Viết phương trình tiếp tuyến đi qua điểm A cho trước
- Viết phương trình tiếp tuyến biết hệ số góc k
2.1. Phương trình tiếp tuyến tại tiếp điểm M(x0,y0) có dạng:
y = f‘(x0)(x−x0) + y0 (1)
Trong đó: f‘(x0) là đạo hàm của hàm số tại điểm x0.
x0; y0 là hoành độ, tung độ của tiếp điểm M.
Như vậy với bài tập yêu cầu viết phương trình tiếp tuyến thì ta phải tìm 3 đại lượng là: f′(x0); x0 và y0.
Phương trình tiếp tuyến tại tiếp điểm:
Để viết phương trình tiếp tuyến tại tiếp điểm cho trước M(x0, y0)
Cách làm: Bài toán yêu cầu viết phương trình tiếp tuyến tại tiếp điểm M(x0,y0) thì công việc cần làm là tìm f′(x0); x0 và y0, trong đó x0, y0 chính là tọa độ của điểm M, vì vậy chỉ cần tính f′(x0), rồi thay vào phương trình (1) là xong.
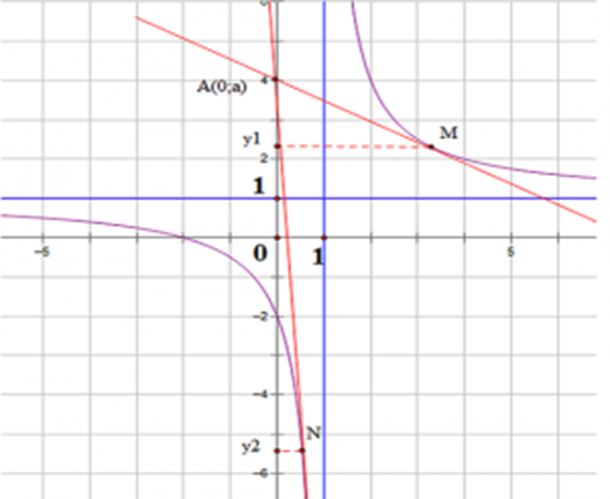
2.2. Phương trình tiếp tuyến đi qua một điểm
Cho đồ thị hàm số y=f(x), viết phương trình tiếp tuyến Δ của đồ thị hàm số biết tiếp tuyến đi qua A(a,b)
Phương pháp:
Gọi phương trình tiếp tuyến của Δ có dạng: y = f’x_{0}(x – x_{0}) + y_{0} (2)
Và có tiếp điểm M0(x0,y0)
Vì A(a,b) thuộc tiếp tuyến nên thay tọa độ A vào phương trình ta có:
b=f′x0(a–x0)+fx0 với fx0=y0
Phương trình này chỉ chứa ẩn x0, do đó chỉ cần giải phương trình trên để tìm x0.
Sau đó sẽ tìm được f′x0 và y0.
Tới đây phương trình tiếp tuyến của chúng ta đã tìm được.

2.3. Phương trình tiếp tuyến có hệ số góc k
Để viết phương trình tiếp tuyến Δ của đồ thị (C) y = f(x) khi hệ số góc k ta làm theo các bước sau:
- Bước 1: Tính đạo hàm f’(x)
- Bước 2: Giải phương trình f’(x) = k để tìm hoành độ x0 của tiếp điểm. Từ đây suy ra tọa độ điểm M0(x0;y0) với y0=f(x0)
- Bước 3: Viết phương trình tiếp tuyến Δ tại tiếp điểm M0(x0;y0):
y=f′(x0)(x–x0)+y0
*Chú ý: Tính chất của hệ số góc k của tiếp tuyến
- Tiếp tuyến song song với đường thẳng y = ax + b thì k = a
- Tiếp tuyến vuông góc với đường thẳng y = ax + b thì k= −a
Phương trình tiếp tuyến của đồ thị hàm số là một trong những kiến thức toán cơ bản để ôn thi kết thúc THPT. Muốn thành thạo dạng toán phương trình tiếp tuyến này, không có cách nào khác là ta phải làm bài tập nhiều để ghi nhớ rõ ràng các phương pháp. Xem thêm các kiến thức về bài toán hàm số và vẽ đồ thị hàm số. Hy vọng với những chia sẻ trên đây, sẽ giúp các em cũng cố kiến thức và làm bài tập phương trình tiếp tuyến thành thạo.
