Table of Contents
Định lý hàm cosin là một định lý trong giải tích, về giá trị cosin của một góc nằm trong khoảng từ 0 đến π/2 luôn nhỏ hơn hoặc bằng 1. Định lý này cung cấp một giới hạn trên cho giá trị của hàm cosin và được áp dụng rộng rãi trong các bài toán liên quan đến tam giác và lượng giác. Vì vậy, định lý hàm cosin là một trong những kiến thức quan trọng trong suốt quá trình học toán ở trường trung học phổ thông. Nhằm giúp các em học sinh dễ dàng ghi nhớ và áp dụng định lý Cosin, VOH Giáo dục đã tổng hợp tất cả kiến thức gồm định lý, hệ quả và tính ứng dụng của nới, mời các em tham khảo:
1. Định lý hàm cosin trong tam giác
Trong một tam giác, ta phát biểu định lý hàm cosin như sau: Trong một tam giác, bình phương một cạnh bằng tổng của hai cạnh kia trừ đi hai lần tích của chúng với cosin của góc xen giữa hai cạnh đó.
Trong tam giác ABC, với AB = c, BC = a, AC = b ta có:

Như vậy, trong một tam giác nếu biết được hai cạnh và góc xen giữa ta sẽ tính được độ dài của cạnh còn lại.
Chứng minh định lý hàm số cosin
Để chứng minh định lý này bạn có thể áp dụng phương pháp dưới đây:
Cho tam giác ABC với BC = a, AC = b, AB = c.
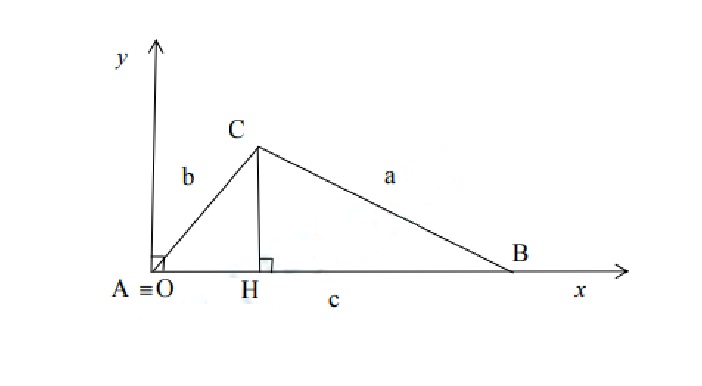

2. Hệ quả định lý hàm cosin
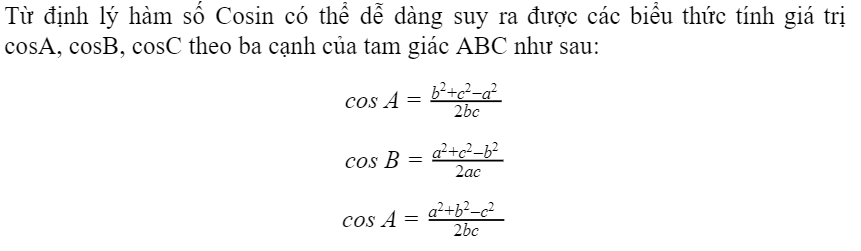
Như vậy hệ quả của định lý hàm cosin cho thấy nếu biết được độ dài của 3 cạnh ta sẽ tính được số đo của các góc. Hay có thể hiểu đơn giản rằng định lý hàm số cosin sẽ giúp ta tính được độ dài của cạnh thì hệ quả của định lý này sẽ giúp chúng ta tính được số đo của góc.
Bên cạnh đó, việc áp dụng định lý hàm số Cosin có thể giúp ta tìm được độ dài các đường trung tuyến theo ba cạnh của một tam giác. Cụ thể:
Trong tam giác ABC, với AB = c, BC = a, AC = b. Nếu đặt các đường trung tuyến kẻ từ các đỉnh A, B, C lần lượt là
3. Ứng dụng của định lý hàm cosin
Định lý hàm cosin là một trong những phần kiến thức cơ bản, xuyên suốt trong chương trình toán học phổ thông. Một số ví dụ về ứng dụng của định lí cosin trong giải toán các bạn có thể tham khảo:

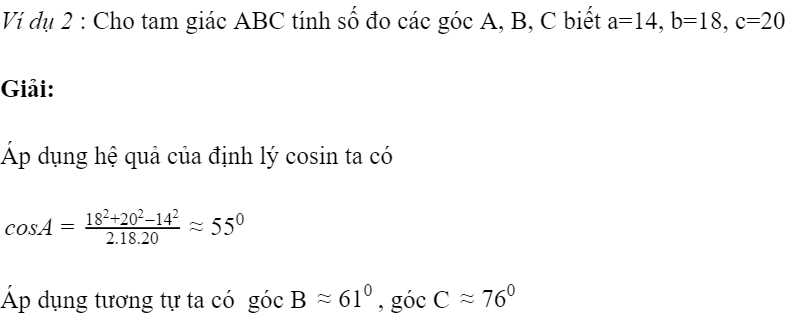
Ngoài ra, có thể áp dụng định lý hàm cosin để tính tam giác trong thực thế. Trong thực tế có nhiều bài toán yêu cầu tính chiều cao của một cây cao nào đó hay một tòa nhà nào đó mà ta không thể trèo lên đến đỉnh của nó để đo trực tiếp được. Chẳng hạn như muốn đo chiều cao của tháp Eiffel ta cũng không thể trèo lên đỉnh của nó mà kéo thước dây để đo trực tiếp được. Vậy để đo chiều cao của nó thì ta sẽ áp dụng định lý hàm số cos vào việc giải tam giác để tính chiều cao theo yêu cầu.
Những chia sẻ về định lý hàm cosin từ VOH Giáo dục vừa cung cấp mong rằng có thể giúp các em học sinh hiểu hơn về phần kiến thức này. Từ đó có thể dễ dàng áp dụng giải toán.
