Công thức tính độ dài đoạn thẳng đầy đủ & bài tập áp dụng

Trong chương trình THPT, tri thức về hệ trục tọa độ Oxyz trong không gian được xem là khá quen thuộc vì chúng ta được tiếp cận với hình học Oxy. Như vậy nói về tính chất cũng như mối quan hệ giữa các điểm trong không gian có sự khác biệt so với trong hình học phẳng hay không? Chủ đề này phần nào đó sẽ trả lời cho câu hỏi đó thông qua công thức tính độ dài đoạn thẳng. VOH Giáo Dục sẽ chia sẻ công thức tính độ dài đường thẳng kèm với ví dụ để các bạn cùng tham khảo nhé.

1. Khái quát hệ trục tọa độ trong không gian để sử dụng xây dựng công thức tính độ dài đoạn thẳng

Tri thức Toán về hệ trục tọa độ trước chủ đề này chỉ làm việc trên mặt phẳng, khi đó ta được học về hệ trục tọa độ Oxy. Tuy nhiên, trong thực tế không thể mô tả vật thể trong không gian bằng hình học phẳng. Chính vì vậy để có thể nêu rõ tính chất của các khối đa diện, chúng ta cần xây dựng hệ trục tọa độ Oxyz.

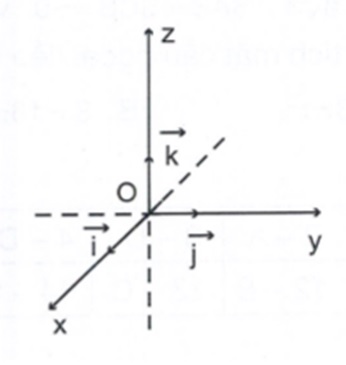
Trong không gian hệ gồm ba trục tọa độ x'Ox, y'Oy, z'Oz đôi một vuông góc với nhau được gọi là hệ trục tọa độ vuông góc trong không gian.

• Điểm O được gọi là gốc tọa độ.
• Trục Ox: trục hoành.
• Trục Oy: trục tung.
• Trục Oz: trục cao.

Các mặt phẳng chứa hai trục tọa độ gọi là các mặt phẳng tọa độ, kí hiệu là (Oxy), (Oyz), (Ozx).

Gọi  (1;0;0),  (0;1;0),  (0;0;1) lần lượt là ba vecto đơn vị trên ba trục Ox, Oy, Oz.

» Xem thêm: Hệ tọa độ trong không gian và những công thức quan trọng

2. Mô tả tọa độ một điểm từ đó xây dựng công thức tính độ dài đoạn thẳng

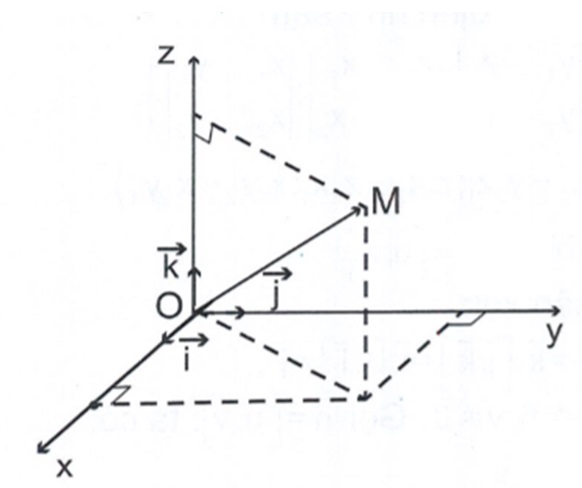
Với mọi điểm M, tồn tại duy nhất bộ ba số (x; y; z) sao cho . Ta gọi bộ ba số (x; y; z) là tọa độ điểm M.

Kí hiệu: M(x; y; z) hay M = (x; y; z).

Do đó ⇔ M(x; y; z).

Nếu điểm M có tọa độ là (x; y; z) thì x, y, z lần lượt được gọi là hoành độ, tung độ và cao độ của điểm M.

Nhận xét:

Điểm M thuộc các trục Ox, Oy, Oz:

M ∈ Ox ⇔ M(x; 0; 0); M ∈ Oy ⇔ M(0; y; 0)

Điểm M thuộc mặt phẳng (Oxy) có z = 0, thuộc mặt phẳng (Oyz) có x = 0, thuộc mặt phẳng (Oxz) có y = 0.

Biểu thức tọa độ của điểm:

Cho bốn điểm A(x_A; y_A; z_A), B(x_B; y_B; z_B), C(x_C; y_C; z_C), D(x_D; y_D; z_D)

Ta có:

• = (x_B - x_A; y_B - y_A; z_B - z_A)

• AB =

• Trung điểm I của AB có tọa độ là:

• I

• Trọng tâm G của tam giác ABC có tọa độ là:

• G

• Điểm N của AB theo tỉ số k:

• =  ⇒ N

∗ Ví dụ

• = ⇔ = (3; -1; -3) ⇔ M (3; -1; -3)

• = ⇔ = (2; -1; 0) ⇔ N (2; -1; 0)

• = ⇔ = ⇔ P

3. Mô tả tọa độ của vectơ từ đó xây dựng công thức tính độ dài đoạn thẳng

Trong không gian Oxyz, với mọi vecto tồn tại duy nhất bộ ba số (x; y; z) sao cho . Ta gọi bộ ba số (x; y; z) là tọa độ của vecto . Kí hiệu: hoặc .

Biểu thức tọa độ các phép toán trên vecto:

Cho hai vecto , , ta có:

• = (x₁ + x₂; y₁ + y₂; z₁ + z₂)

• = (x₁ - x₂; y₁ - y₂; z₁ - z₂)

• = (kx₁; ky₁; kz₁), k ∈ R

Độ lớn của vecto:

 • =

Tích vô hướng của hai vecto:

• = x₁x₂ + y₁y₂ + z₁z₂

Góc giữa hai vecto:

• cos = =

Với ≠ 0

Đặc biệt:

Hai vecto bằng nhau

⇔

Hai vecto và cùng phương khi và chỉ khi , k ∈ R

• ⇔ = 0 ⇔ x₁x₂ + y₁y₂ + z₁z₂ = 0

∗ Ví dụ

• Cho hai vecto (1; -3; 4), (-2; 3; 5)

• Độ lớn của vecto:

• Tích vô hướng của hai vecto:

• Góc giữa hai vecto:

4. Công thức tính độ dài đoạn thẳng trong không gian oxyz

Nhắc lại công thức tính độ dài đoạn thẳng trong hình học phẳng:

Cho vectơ = (u₁; u₂) 

• Độ lớn của vectơ

Cho hai điểm A (x_A; y_A), B (x_B; y_B)

• = (x_B - x_A; y_B - y_A)

• AB = =

Liên hệ đến công thức tính độ dài đoạn thẳng trong không gian:

• Cho vecto (x₁; x₂; x₃)

Độ lớn của vecto:

•

∗ Ví dụ minh họa

•

Độ lớn của vecto

•

Cho hai điểm

•

• AB =

Cho hai điểm A (1; 2; -3), B (2; -2; 1)

•

•

5. Bài tập áp dụng công thức tính độ dài đoạn thẳng lớp 10

Bài 1: Trong không gian với hệ trục tọa độ Oxyz, cho các vecto : = (1; 2; -3), = (2; 1; 1), , = (3; -1; 0). Vecto nào có độ dài lớn nhất ?

A.

B.

C.

D.

Bài 2: Trong không gian với hệ trục tọa độ Oxyz, cho ba điểm A (1; 1; 1), B (0; 0; 1), C (3; 1; 1). Tính độ dài đường chéo BD.

A. 1

B. 2

C. 3

D. 4

Bài 3: Trong không gian với hệ trục tọa độ Oxyz, cho bốn điểm A (0; 2; -2), B (-3; 1; -1), C (4; 3; 0), D (1; 2; m). Tìm m để A, B, C, D đồng phẳng. Khi đó độ dài đoạn thẳng AD là bao nhiêu?

A. 5

B. 10

C.

D.

Bài 4: Trong không gian với hệ trục tọa độ Oxyz, cho ba điểm A (-1; 0; 3), B (2; -2; 0), C (-3; 2; 1). Chu vi tam giác ABC bằng:

A.

B.

C.

D.

Bài 5: Trong không gian với hệ trục tọa độ Oxyz, cho vecto = (a; b; c). Khi đó độ dài của được tính theo công thức nào sau đây?

A.

B.

C. a + b + c

D. a² + b² + c²

Kết luận: Chủ đề lớp 10 này thường hiếm xuất hiện trong đề thi THPTQG. Tuy nhiên xét về kiến thức thì đây là kiến thức nền tảng giúp các bạn làm quen cũng như phát triển ở các dạng toán nâng cao sau đó. Ở các ví dụ trên là các bài tập thường xuyên xuất hiện đòi hỏi chúng ta phải sử dụng công thức tính độ dài đoạn thẳng.

Chịu trách nhiệm nội dung: GV Nguyễn Thị Trang