Hình đa diện đều là gì? Cách nhận biết hình đa diện đều loại {3; 5}, {3; 3}, {4; 3}, {3; 4}, {5; 3}

Trong chương trình Toán học bậc THPT, phần Hình học không gian 11 đã giúp chúng ta xây dựng các hình từ các điểm, đường thẳng, mặt phẳng. Như vậy làm cách nào để phân biệt sự khác nhau giữa các hình đa diện đó với nhau? Và nếu cùng là khối đa diện thì tính chất nào để xây dựng lên một hình đa diện đều? Chủ đề này sẽ giúp chúng ta mô tả các hình khối một cách chi tiết nhất.

1. Nhắc lại khái niệm hình đa diện

 ∗ Hình đa diện

Hình đa diện (gọi tắt là đa diện) là hình được tạo bởi một số hữu hạn các đa giác phẳng thỏa mãn hai điều kiện sau:

• Hai đa giác phân biệt chỉ có thể hoặc không có điểm chung hoặc có đỉnh chung hoặc có một cạnh chung.

• Mỗi cạnh của đa giác nào cũng là cạnh chung của đúng hai đa giác.

2. Tổng hợp các đặc điểm, tính chất có liên quan đến hình đa diện đều

Phần không gian giới hạn bởi hình đa diện nào đó sẽ là khối đa diện.

Mỗi đa diện sẽ chia các điểm còn lại của khối thành 2 miền gồm miền trong và miền ngoài của nó không giao nhau. Trong đó, chỉ có miền ngoài sẽ chứa trọn một đường thẳng nào đó. Còn các điểm của miền trong là các điểm trong và các điểm ngoài của đa diện là các điểm thuộc miền ngoài.

• Hợp của hình đa diện và miền trong của nó chính là khối đa diện.

• Phép dời hình và sự bằng nhau đều có trong khối đa diện. Trong đó:

• Phép biến hình trong không gian chính là quy tắc đặt tương ứng mỗi điểm M với điểm M’ xác định duy nhất trong không gian.

• Phép biến hình trong không gian được gọi là phép dời hình nếu bảo toàn khoảng cách giữa 2 điểm tùy ý.

• Thực hiện liên tiếp nhiều phép dời hình sẽ được 1 phép dời hình.

• Phép dời hình sẽ biến các cạnh, đỉnh, mặt của đa diện này thành của đa diện kia hay biến một đa diện thành một đa diện khác.

• Các phép dời hình trong không gian, bao gồm:

   - Phép biến hình biến điểm M thành M’ thỏa mãn điều kiện gọi là phép dời hình tịnh tiến theo vector

  - Phép biến hình biến mọi điểm thuộc (P) thành chính nó và biến điểm M không thuộc (P) thành điểm M’ thỏa mãn điều kiện (P) là mặt phẳng trung trực của MM’ gọi là phép đối xứng qua mặt phẳng (P). Và (P) sẽ được gọi là mặt phẳng đối xứng của H khi phép đối xứng qua mặt phẳng P biến hình H thành chính nó.

  - Phép đối xứng tâm O xảy ra khi phép biến hình biến điểm O thành chính nó và biến điểm M khác O thành điểm M’ thỏa mãn điều kiện O là trung điểm của MM’. Nếu phép đối xứng tâm O biến hình đa diện thành chính nó thì O sẽ là tâm đối xứng của hình đa diện.

  - Phép biến hình mọi điểm thuộc d thành chính nó và biến điểm M không thuộc d thành M’ thỏa mãn điều kiện d là trung trực của MM’ gọi là phép đối xứng qua đường thẳng d, gọi là phép đối xứng qua trục d. Nếu nó biến hình đa diện thành chính nó, d được gọi là trục đối xứng của nó.

+ Nếu một phép dời hình biến hình này thành hình kia sẽ được gọi là hai hình bằng nhau.

+ Nếu hai tứ diện có các cạnh tương ứng bằng nhau thì hai tứ diện được gọi là bằng nhau.

 + Nếu H1 và H2 hợp thành khối đa diện (H) khi H1 và H2 không có điểm trong chung, chúng ta chia thành 2 khối đa diện H1 và H2 từ khối đa diện hay ngược lại lắp ghép 2 khối đa diện này với nhau tạo thành khối đa diện H.

+ Mỗi khối đa diện đều phân chia được thành các khối tứ diện.

3. Hình đa diện đều là gì?

Hình đa diện đều (gọi tắt là đa diện đều) là hình được tạo bởi một số hữu hạn các đa giác phẳng đều thỏa mãn hai điều kiện sau:

• Hai đa giác phân biệt chỉ có thể hoặc không có điểm chung hoặc có đỉnh chung hoặc có một cạnh chung.

• Mỗi cạnh của đa giác nào cũng là cạnh chung của đúng hai đa giác.

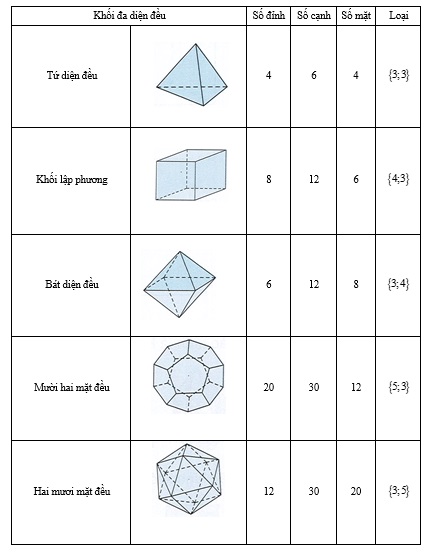
4. Số mặt, số cạnh, số đỉnh về các hình đa diện đều đặc biệt

4.1. Hình đa diện đều loại {3; 5}, {3; 3}, {4; 3}, {3; 4}, {5; 3}

p.Đ = 2.C = n.M

Đ + M = C + 2

4.2. Mặt phẳng đối xứng

5. Các dạng bài tập về hình đa diện đều

Bài 1: Hình đa diện nào dưới đây không có tâm đối xứng?

A. Tứ diện đều

B. Bát diện đều

C. Hình lập phương

D. Lăng trụ lục giác đều

Bài 2: Trong các phát biểu sau, phát biểu nào sai:

A. Hình chóp đều là hình chóp có tất cả các cạnh bên bằng nhau và đáy là đa giác đều.

B.Trong một hình chóp đều các góc giữa một cạnh bên và mặt đáy thì bằng nhau.

C. Hình chóp đều là hình chóp có đáy là đa giác đều và chân đường cao trùng với tâm của đáy.

D. Hình chóp đều là hình chóp có tất cả các cạnh bằng nhau.

Bài 3: Một hình chóp đều có 46 cạnh có bao nhiêu mặt?

A. 24

B. 46

C. 69

D. 25

Bài 4: Hình tứ diện đều có bao nhiêu mặt phẳng đối xứng? 

A. 1

B. 4

C. 3

D. 6

Bài 5: Hình bát diện đều có tất cả bao nhiêu mặt phẳng đối xứng ?

A. 5

B. 6

C. 9

D. 8

Trong kỳ thi THPTQG, các dạng toán liên quan về phần khối đa diện này thuộc những câu ở mức độ nhận biết, thông hiểu. Tuy nhiên đây là một nội dung rất dễ mất điểm nếu chúng ta không hiểu rõ bản chất. Việc phân biệt được hình đa diện đều, các khối đa diện và tính chất còn giúp chúng ta vẽ hình và ghi dữ kiện cho các bài toán liên quan đến hình học không gian chính xác nhất.

Chịu trách nhiệm nội dung: GV Nguyễn Thị Trang