Table of Contents
Trong chương trình toán bậc THPT, nội dung về khối đa diện và các bài toán liên quan đến thể tích khối đa diện rất phổ biến trong các kì thi. Như vậy khối đa diện đều là gì? Có bao nhiêu loại khối đa diện đều? Thì chủ đề này sẽ trình bày chi tiết về vấn đề đó.
1. Khối đa diện đều là gì?
Khối đa diện đều là một khối đa diện lồi có hai tính chất sau đây:
• Các mặt là những đa giác đều n cạnh.
• Mỗi đỉnh là đỉnh chung của đúng p cạnh. Khối đa diện đều như vậy gọi là khối đa diện đều loại
Gọi Đ là tổng số đỉnh, C là tổng số cạnh và M là tổng các mặt của khối đa diện đều loại

2. Các loại khối đa diện đều
p.Đ = 2.C = n.M
Đ + M = C + 2
Trong đó:
• số đỉnh (Đ)
• số mặt (M)
• số cạnh (C)
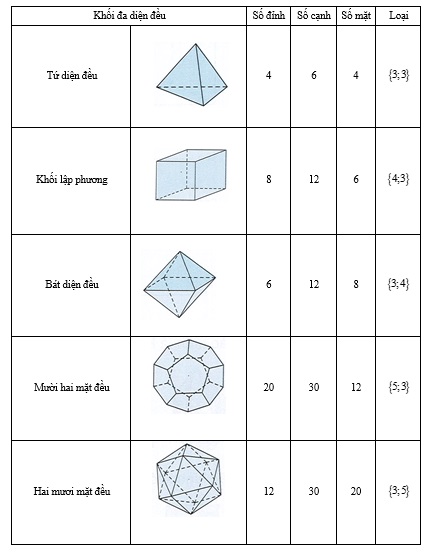
2.1. Khối đa diện đều loại {3;3}
Là tứ diện đều. Có số đỉnh là 4, số cạnh là 6, số mặt là 4
Mỗi mặt là một tam giác đều.
2.2. Khối đa diện đều loại {4;3}
Là khối lập phương. Có số đỉnh là 8, số cạnh là 12, số mặt là 6
Mỗi mặt là một hình vuông.
2.3. Khối đa diện đều loại {3;4}
Là bát diện đều. Có số đỉnh là 6, số cạnh là 12, số mặt là 8
Mỗi mặt là một tam giác đều.
2.4. Khối đa diện đều loại {5;3}
Là mười hai mặt đều. Có số đỉnh là 20, số cạnh là 30, số mặt là 12
Mỗi mặt là một ngũ giác đều.
2.5. Khối đa diện đều loại {3;5}
Là hai mươi mặt đều. Có số đỉnh là 12, số cạnh là 30, số mặt là 20
Mỗi mặt là một tam giác đều.
3. Mặt phẳng đối xứng của khối đa diện đều
| Hình | Số mặt phẳng đối xứng |
Tứ diện đều | 6 |
Hình lập phương | 9 |
Hình chóp tứ giác đều | 4 |
Hình hộp chữ nhật | 3 |
Bát diện đều | 9 |
4. Các dạng bài tập về khối đa diện đều
Bài 1: Tâm các mặt hình lập phương tạo thành các đỉnh của khối đa diện nào sau đây?
A. Khối chóp lục giác đều
B. Khối bát diện đều
C. Khối lăng trụ tam giác đều
D. Khối tứ diện đều
ĐÁP ÁN
∗ Phương pháp
Vẽ hình
∗ Cách giải
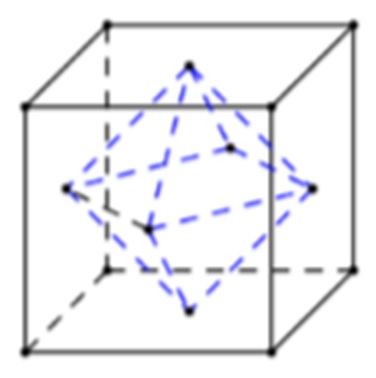
→ Chọn câu B.
Bài 2: Cho khối đa diện đều giới hạn bởi hình đa diện (H), khẳng định nào sau đây là sai?
A. Các mặt của (H) là những đa giác đều có cùng số cạnh.
B. Mỗi cạnh của một đa giác của (H) là cạnh chung của nhiều hơn hai đa giác.
C. Khối da diện đều (H) là một khối đa diện lồi.
D. Mỗi đỉnh của (H) là đỉnh chung của cùng một số cạnh.
ĐÁP ÁN
∗ Phương pháp
Sử dụng định nghĩa khối đa diện đều.
∗ Cách giải
Khối đa diện đều là một khối đa diện lồi có hai tính chất sau đây:
- Các mặt là những đa giác đều và có cùng số cạnh.
- Mỗi đỉnh là đỉnh chung của cùng một số cạnh.
Từ định nghĩa khối đa diện đều ta thấy A, C, D đúng. Vậy B sai.
→ Chọn câu B.
Bài 3: Khối bát diện đều là một khối đa diện lồi loại:
A. {5;3}.
B. {4;3}.
C. {3;4}.
D. {3;5}.
ĐÁP ÁN
∗ Phương pháp
Khối đa diện đều mà mỗi mặt là đa giác n cạnh và mỗi đỉnh là đỉnh chung của p cạnh được gọi là khối đa diện đều loại {n; p}.
∗ Cách giải
Khối bát diện đều là khối đa diện đều thuộc loại {3;4}.
→ Chọn câu C.
Bài 4: Có tất cả bao nhiêu loại khối đa diện đều?
A. 3
B. 5
C. 6
D. 4
ĐÁP ÁN
∗ Phương pháp
Sử dụng lý thuyết về khối đa diện đều (chỉ xét khối đa diện lồi)
∗ Cách giải
Có tất cả 5 khối đa diện lồi đều: tứ diện đều, khối lập phương, khối tám mặt đều, khối mười hai mặt đều, khối hai mươi mặt đều.
→ Chọn câu B.
Bài 5: Khối đa diện đều có 12 mặt thì số cạnh là:
A. 60
B. 30
C. 12
D. 24
ĐÁP ÁN
∗ Phương pháp
Sử dụng tính chất của khối 12 mặt đều.
∗ Cách giải
Khối 12 mặt đều có 12 mặt, 20 đỉnh và 30 cạnh.
→ Chọn câu B.
Khi học chương này các bạn cần đặc biệt lưu ý về tính chất cũng như phân biệt được các khối đa diện với nhau. Kiến thức của chủ đề này là cơ sở để xây dựng các bài toán về thể tích, về tỉ số thể tích. Hệ thống bài tập về khối đa diện đều xoay quanh hai dạng: thứ nhất là về cơ sở lý thuyết, thứ hai là về vận dụng tính chất để vẽ hình giải quyết các bài toán ở mức độ vận dụng – vận dụng cao. Chúc các bạn học tốt!
Chịu trách nhiệm nội dung: GV Nguyễn Thị Trang
