Table of Contents
- I. Tổng hợp lý thuyết về hàm số y=ax
- II. Các dạng bài tập liên quan đến hàm số y=ax
- 1. Nhận dạng hàm số, vẽ đồ thị hàm số y=ax (a ≠ 0) khi biết hệ số a
- 2. Xét xem một điểm bất kì cho trước có thuộc đồ thị hàm số y=ax không?
- 3. Cho đồ thị hàm số y=ax đi qua một điểm bất kì cho trước. Tìm hệ số a.
- 4. Cho biết giá trị của hàm số. Yêu cầu tính giá trị của biến số
- 5. Cho giá trị của biến số, tìm giá trị của hàm số
- 6. Bài toán về xét sự đồng biến hay nghịch biến của hàm số y=ax
- III. Một số bài tập vận dụng về hàm số y=ax
Hàm số y=ax (a ≠ 0) là một trong những hàm số cơ bản và dễ vẽ đồ thị nhất trong các loại hàm số mà chúng ta được học. Vậy hàm số y=ax là hàm số như thế nào? Tại sao đồ thị hàm số y=ax lại dễ vẽ? và các bài tập về chủ đề này có phương pháp để làm không? Chúng ta sẽ cùng nhau giải đáp thắc mắc này qua bài viết dưới đây nhé.
I. Tổng hợp lý thuyết về hàm số y=ax
1. Đồ thị hàm số y=ax
- Đồ thị của hàm số y=ax (a ≠ 0) là một đường thẳng đi qua gốc tọa độ.
*Chú ý: - Giao điểm của các đồ thị hàm số có dạng y=ax chính là gốc tọa độ O(0; 0)
*Cách nhận biết hàm số có dạng y=ax:
- Hàm số chỉ có một biến số là x và chỉ có hệ số đứng trước x và không có hệ số tự do.
Chẳng hạn như hàm số y = 8x là hàm số có dạng y=ax vì hàm số này chỉ có một biến số là x và hệ số trước x là 8 mà không có hệ số tự do nào.
2. Phương pháp vẽ đồ thị hàm số y=ax (a ≠ 0)
Để vẽ đồ thị hàm số y=ax (a ≠ 0) ta làm như sau:
- Bước 1: Vẽ hệ trục tọa độ Oxy
- Bước 2: Xác định một điểm thuộc đồ thị và khác điểm gốc tọa độ O.
- Bước 3: Vẽ một đường thẳng đi qua điểm vừa xác định ở bước 1 và qua gốc tọa độ.
Đường thẳng vừa vẽ chính là đồ thị hàm số y=ax mà chúng ta cần vẽ.
Ví dụ minh họa:
Cho hàm số y =
Giải:
Ta áp dụng cách vẽ đồ thị hàm số y=ax ở trên.
- Bước 1: Vẽ hệ trục tọa độ Oxy
- Bước 2: Tìm một điểm thuộc đồ thị hàm số y =
x nhưng khác điểm gốc tọa độ O:
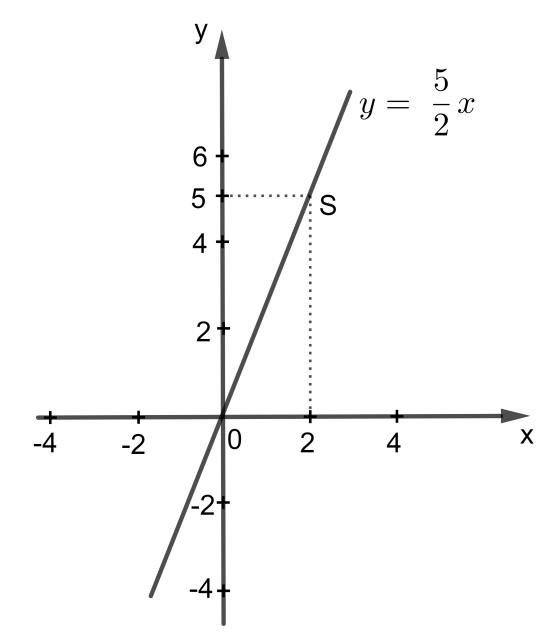
Ta cho x = 2 suy ra y = 5
Vậy ta có điểm S(2; 5) thuộc đồ thị hàm số y =
- Bước 3: Kẻ một đường thẳng đi qua hai điểm S(2; 5) và đi qua gốc tọa độ O(0; 0)
Khi đó đường thẳng vừa vẽ được chính là đồ thị của hàm số y =
II. Các dạng bài tập liên quan đến hàm số y=ax
1. Nhận dạng hàm số, vẽ đồ thị hàm số y=ax (a ≠ 0) khi biết hệ số a
*Phương pháp giải: Dựa vào định nghĩa để nhận biết một hàm số có phải là hàm số y=ax hay không?
Và dựa vào phương pháp vẽ đồ thị hàm số y=ax để vẽ.
*Ví dụ: Trong các hàm số sau, hàm số nào có dạng y=ax. Hãy vẽ đồ thị hàm số đó.
a. y = -4x + 3
b. y = 2x
c. y = 2(x - 1)
Giải:
Hàm số có dạng y=ax (a ≠ 0) là hàm số y = 2x.
Vẽ đồ thị hàm số y = 2x:
- Vẽ hệ trục tọa độ Oxy
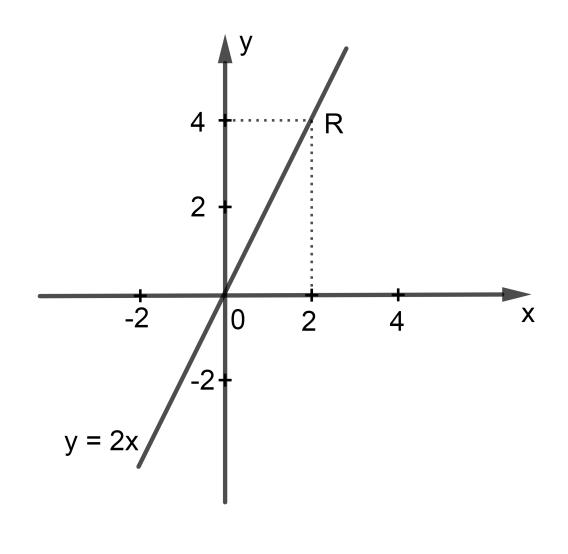
- Cho x = 2 suy ra y = 4.
Vậy đồ thị hàm số trên đi qua 2 điểm R(2; 4) và O(0; 0)
- Kẻ đường thẳng đi qua hai điểm trên ta sẽ được đồ thị hàm số y = 2x cần vẽ.
2. Xét xem một điểm bất kì cho trước có thuộc đồ thị hàm số y=ax không?
*Phương pháp giải: Ta thay các giá trị x, y tương ứng của điểm đó vào hàm số y=ax.
- Nếu thỏa mãn hàm số y=ax thì điểm đó thuộc đồ thị hàm số.
- Nếu không thỏa mãn hàm số y=ax thì điểm đó không thuộc đồ thị hàm số.
*Ví dụ: Cho điểm W(2; 1), K(-1; 4). Xét xem hai điểm trên có thuộc đồ thị hàm số y = 5x + 9 không?
Giải:
Ta thay x = 2, y = 1 vào y = 5x + 9, ta được: 1 = 5.2 + 9 ( vô lý)
Vậy điểm W(2;1) không thuộc đồ thị hàm số y = 5x + 9
Tương tự, ta thay x = -1, y = 4 vào y = 5x + 9, ta được: 4 = 5.(-1) + 9 (thỏa mãn)
Vậy điểm K(-1; 4) thuộc đồ thị hàm số y = 5x + 9
3. Cho đồ thị hàm số y=ax đi qua một điểm bất kì cho trước. Tìm hệ số a.
*Phương pháp giải: Thay tọa độ của điểm cho trước vào đồ thị hàm số y=ax, từ đó suy ra hệ số a.
*Ví dụ: Cho điểm P(2; 8) thuộc đồ thị hàm số y=ax. Hãy tìm hệ số a của đồ thị hàm số trên.
Giải:
Vì điểm P(2; 8) thuộc đồ thị hàm số y=ax nên ta có: 8 = a.2 ⇒ a = 8 : 2 = 4
Vậy hệ số a của y=ax là a = 4
4. Cho biết giá trị của hàm số. Yêu cầu tính giá trị của biến số
*Phương pháp giải: Thay giá trị của hàm số vào đồ thị hàm số y=ax, từ đó tìm ra giá trị của biến số
* Ví dụ: Cho hàm số y = 39x. Hãy tìm giá trị của biến số x biết giá trị của hàm số là y = 78
Giải:
Ta có: y = 39x = 78 ⇒ x = 2
Vậy giá trị của biến số x là: x = 2
5. Cho giá trị của biến số, tìm giá trị của hàm số
*Phương pháp giải: Thay giá trị của biến số vào hàm số y=ax để tìm ra giá trị của hàm số đó.
*Ví dụ: Cho hàm số y = 5x. Hãy tính y(2); y(-9)
Giải:
Ta có: y(2) = 5.2 = 10
y(-9) = 5.(-9) = -45
6. Bài toán về xét sự đồng biến hay nghịch biến của hàm số y=ax
*Phương pháp giải: Hàm số y=ax là hàm số đồng biến khi a > 0 và là hàm số nghịch biến khi a < 0
*Ví dụ: Hãy xét tính đồng biến, nghịch biến của các hàm số sau:
a. y = 2022x
b. y = -10x
Giải:
a. Ta có: a = 2022 > 0 nên hàm số y = 2022x là hàm số đồng biến
b. Ta có: a = -10 < 0 nên hàm số y = -10x là hàm số nghịch biến
III. Một số bài tập vận dụng về hàm số y=ax
Bài 1: Cho hàm số y=ax (a≠ 0)
a. Hãy xác định công thức của hàm số trên biết y tỉ lệ thuận với x và hệ số tỉ lệ của x đối với y là
b. Hãy vẽ đồ thị hàm số trên
ĐÁP ÁN
a. Vì y tỉ lệ thuận với x và hệ số tỉ lệ của x đối với y là
Từ đó suy ra: y = x :
Vậy công thức của hàm số trên là: y =
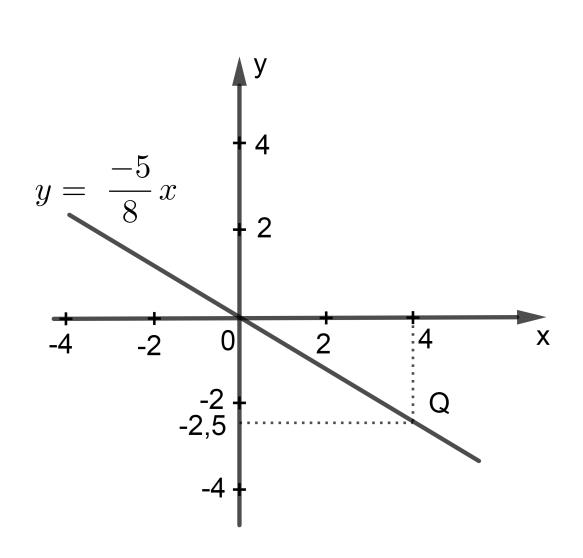
b. Với x = 4 ⇒ y = -2,5
Vậy đồ thị hàm số y =
Bài 2: Cho hàm số y =
a. Hãy giải thích vì sao hàm số trên lại là hàm số nghịch biến
b. Tính giá trị của hàm số trên với các biến số lần lượt là -3; 20
ĐÁP ÁN
a. Hàm số y =
Vì ta có a =
b. Giá trị của hàm số cần tính chính là y và các biến số đã cho chính là x.
Vậy với x = -3, ta có: y =
với x = 20, ta có: y =
Trên đây là các kiến thức liên quan đến hàm số y=ax và đồ thị hàm số y=ax với các dạng bài tập liên quan có phương pháp giải và ví dụ cụ thể. Hy vọng bài viết trên sẽ giúp các bạn học sinh hiểu rõ hơn về hàm số y=ax và có thể từ những kiến thức trên vận dụng vào giải các bài tập thuận lợi hơn.
Chịu trách nhiệm nội dung: GV Nguyễn Thị Trang
