Table of Contents
Như các bạn đã biết, đường trung tuyến là một kiến thức rất quan trọng trong chương trình hình học lớp 7. Vậy thế nào là đường trung tuyến của tam giác? Tính chất ba đường trung tuyến của tam giác như thế nào và nó có các điểm đặc biệt gì? Chúng ta sẽ cùng tìm hiểu trong bài viết này nhé.
1. Đường trung tuyến của tam giác là gì?
Đoạn thẳng AM nối đỉnh A của tam giác ABC với trung điểm M của cạnh BC gọi là đường trung tuyến (xuất phát từ đỉnh A hoặc ứng với cạnh BC) của tam giác ABC.
Mỗi tam giác có ba đường trung tuyến.
Ví dụ: Tam giác ABC có ba đường trung tuyến AM, BN, CP.
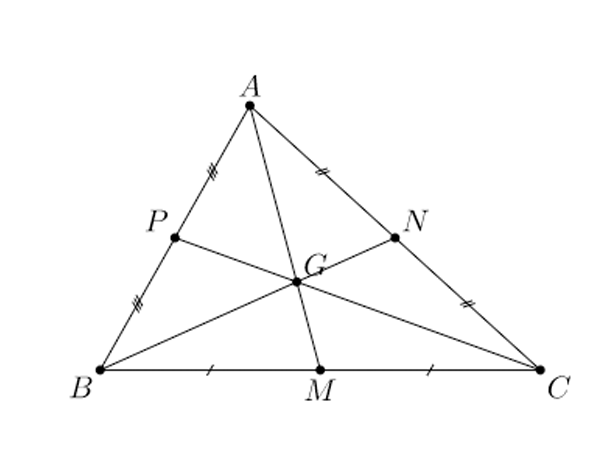
2. Tính chất ba đường trung tuyến của tam giác
Ba đường trung tuyến của một tam giác cùng đi qua một điểm. Điểm đó cách mỗi đỉnh một khoảng bằng
Cụ thể, trong tam giác ABC (hình 4.1), các đường trung tuyến AM, BN, CP cùng đi qua điểm G (hay còn gọi là đồng quy tại điểm G) và ta có:
Điểm G gọi là trọng tâm của tam giác ABC.
3. Các dạng bài tập cơ bản về đường trung tuyến của tam giác lớp 7
3.1. Dạng 1: Chứng minh đường thẳng là đường trung tuyến của tam giác
Bài 1: Cho tam giác MNP cân tại M, có MH vuông góc với NP. Chứng minh MH là đường trung tuyến của tam giác MNP.
ĐÁP ÁN
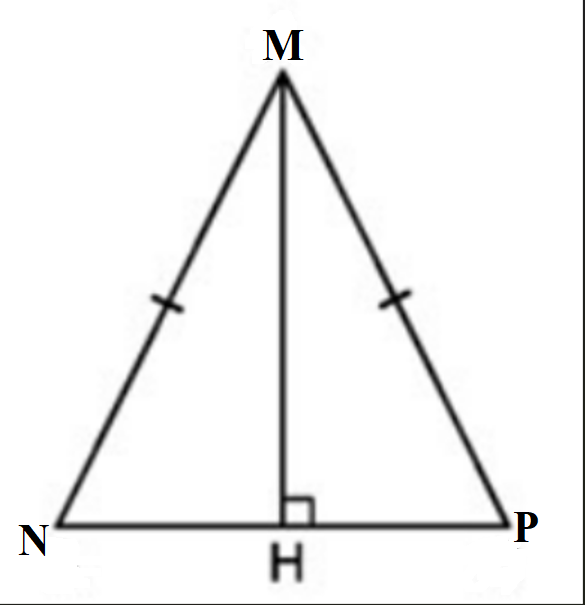
Xét tam giác MNH vuông tại H và tam giác MPH vuông tại H có:
MN = MP ( Vì tam giác MNP cân tại M)
AH là cạnh chung
Do đó,
Suy ra NH = PH (hai cạnh tương ứng)
Suy ra H là trung điểm của NP
Vậy MH là đường trung tuyến của tam giác MNP.
Bài 2: Cho tam giác DEF có M, N lần lượt là trung điểm của DE và DF. Biết FM và EN cắt nhau tại H. Chứng minh DH là đường trung tuyến của tam giác DEF.
ĐÁP ÁN
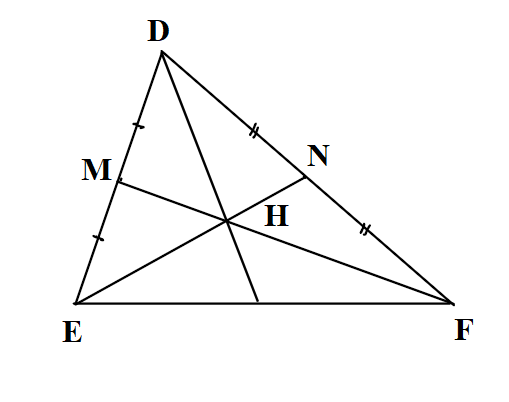
Vì M, N lần lượt là trung điểm của DE và EF nên FM và EN là hai đường trung tuyến của tam giác DMN.
Mà FM và EN cắt nhau tại H nên DH là đường trung tuyến thứ ba của tam giác DEF.
3.2. Dạng 2: Sử dụng tính chất đường trung tuyến của tam giác
Bài 1: Cho tam giác MNP, D là trung điểm của MN. Trên đoạn ND lấy điểm E sao cho NE = 2 ED. Điểm F thuộc tia đối của tia DE sao cho NF = 2 NE. Gọi K là trung điểm của PF và G là giao điểm của EK với MP.
a) Chứng minh G là trọng tâm tam giác EFP.
b) Tính tỉ số
ĐÁP ÁN
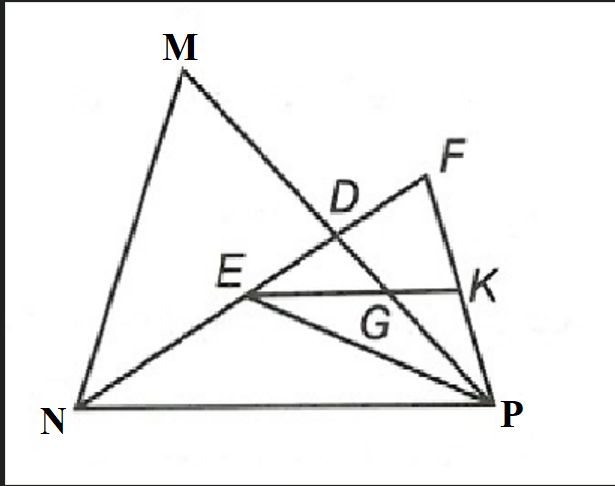
Mà NE = 2 ED nên EF = 2 ED
Vì K là trung điểm của PF nên EK là đường trung tuyến của tam giác EFP.
Tam giác EFP có hai đường trung tuyến PD và EK cắt nhau tại G nên G là trọng tâm tam giác EFP.
b) Vì G là trọng tâm tam giác EFP nên
Bài 2: Cho tam giác ADP có hai đường trung tuyến DE và PF cắt nhau ở G. AG kéo dài cắt PD ở M. Chứng minh MP = MD.
ĐÁP ÁN
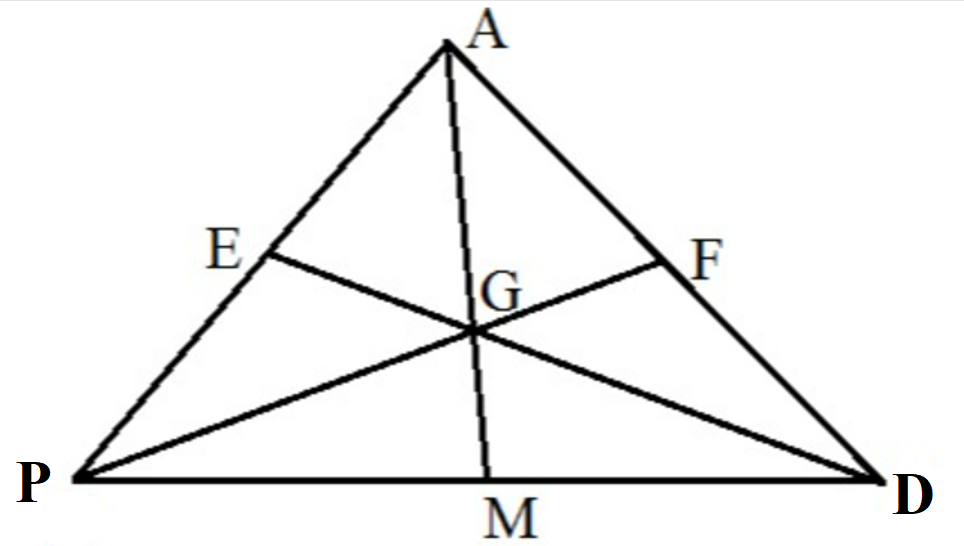
Vì tam giác ADP có hai đường trung tuyến cắt nhau tại G, suy ra G là trọng tâm tam giác ADP.
Mà AM đi qua G nên AM là đường trung tuyến thứ ba.
Suy ra M là trung điểm của DP
Vậy MD = MP.
3.3. Dạng 3: Đường trung tuyến của tam giác cân, tam giác đều, tam giác vuông
Bài 1: Cho tam giác đều DEF có ba đường trung tuyến DM, EN, FP cắt nhau tại O. Chứng minh:
a) DM = EN = FP.
b) OD = OE = OF.
ĐÁP ÁN
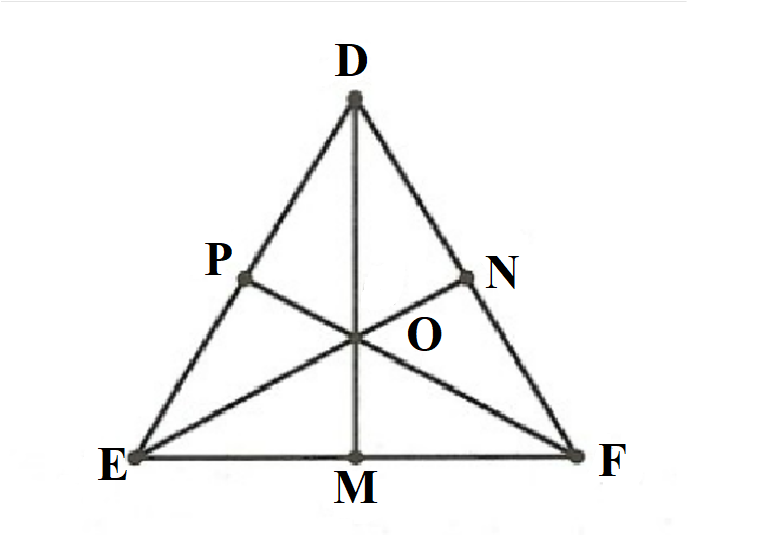
a) Ta có FP, EN là các đường trung tuyến của tam giác DEF
Vì DF = DE (tam giác DEF đều) nên
Xét tam giác EFN và tam giác FEP có:
EF là cạnh chung;
FN = EP ( chứng minh trên)
Do đó,
Chứng minh tương tự ta có DM = EN
Từ đó suy ra DM = EN = FP
b) Vì tam giác DEF có ba đường trung tuyến cắt nhau tại O nên O là trọng tâm tam giác DEF
Vì DM = EN = FP nên
hay OD = OE = OF
Bài 2: Chứng minh rằng trong một tam giác, đường trung tuyến ứng với một cạnh bằng nửa cạnh ấy thì tam giác đó là tam giác vuông.
ĐÁP ÁN
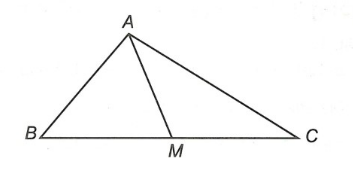
Xét tam giác ABC có trung tuyến
Khi đó tam giác AMB cân tại M và tam giác AMC cân tại M.
Xét tam giác ABC có
nên
Vậy tam giác ABC vuông ở A.
3.4. Dạng 4: Một số bài tập nâng cao về đường trung tuyến của tam giác
Bài 1: Cho hai đường thẳng aa' và bb' cắt nhau tại O. Trên aa' lấy ba điểm A, B, C sao cho OA = AB = BC, trên bb' lấy ba điểm E, M, N sao cho OE = OM = MN. Chứng minh rằng ba đường thẳng AE, BN và CM cùng đi qua một điểm.
ĐÁP ÁN
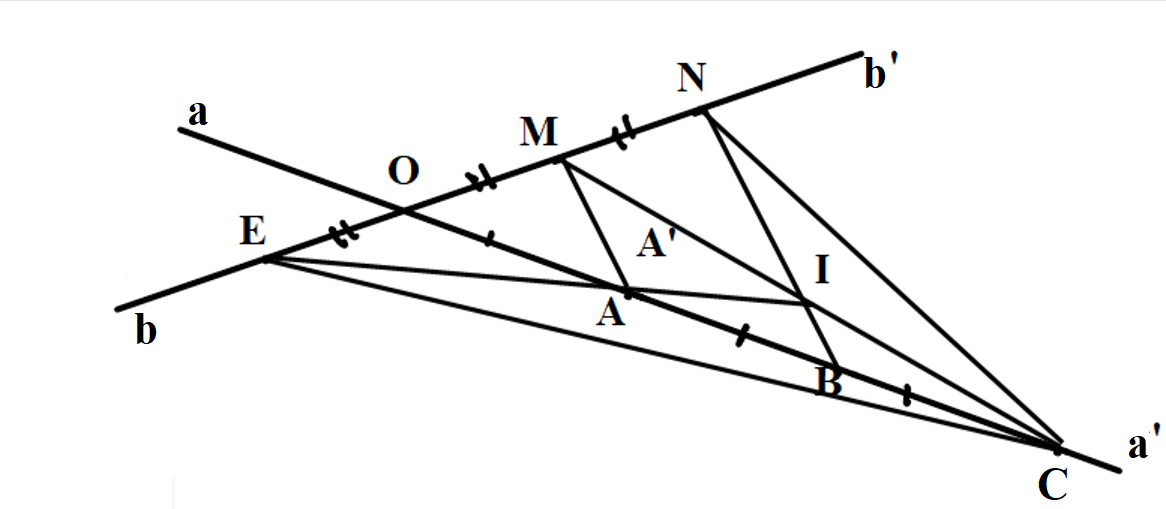
Xét tam giác MEC có OE = OM nên O là trung điểm của EM
Suy ra, CO là đường trung tuyến ứng với cạnh EM của tam giác EMC (1)
Gọi I là trung điểm của MC và A' là giao điểm của EI và CO (2)
Nên EI là đường trung tuyến ứng với cạnh MC của tam giác EMC (3)
Từ (1), (2), (3), suy ra A' là trọng tâm tam giác MCE nên OA'=
mà
Suy ra OA = OA' nên
Ta có, BN // MA và BI // MA suy ra N, I, B thẳng hàng
Vậy ba đường thẳng AE, BN, CM đồng quy tại I
Bài 2: Cho tam giác MNE, ba đường trung tuyến MP, NF, EA cắt nhau ở O. Chứng minh rằng 2 tam giác OEP, OFE có diện tích bằng nhau.
ĐÁP ÁN
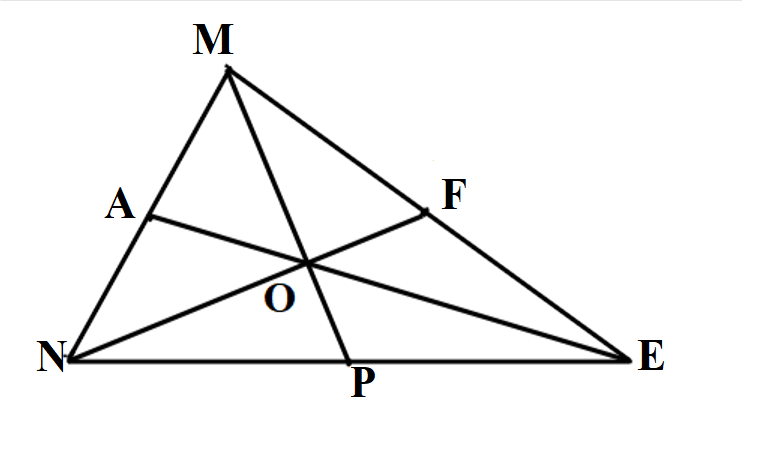
Vì tam giác MNE có ba đường trung tuyến cắt nhau tại O, nên O là trọng tâm tam giác MNE
Suy ra
Hai tam giác OEP và EMP có cùng chiều cao hạ từ đỉnh E xuống MP, và có
Hai tam giác EMP và EMN có cùng chiều cao hạ từ đỉnh M xuống NE và có
Suy ra
Chứng minh tương tự ta có
Vậy
Trên đây là một số kiến thức trọng tâm liên quan đến tính chất 3 đường trung tuyến của tam giác, hy vọng bài viết này sẽ giúp các em hiểu rõ hơn về đường trung tuyến đồng thời áp dụng được vào các bài toán liên quan. Chúc các em học thật tốt nhé.
Chịu trách nhiệm nội dung: GV Nguyễn Thị Trang
