Table of Contents
Tứ giác là hình đã được biết đến trong môn Toán ở cấp Tiểu học. Tuy nhiên ở Lớp 8, chúng ta sẽ đi tìm hiểu chi tiết hơn về định nghĩa, tính chất và các dạng bài tập liên quan đến tứ giác lồi.
1. Tứ giác lồi là gì?
- Tứ giác ABCD là hình gồm bốn đoạn thẳng AB, BC, CD, DA, trong đó bất kì hai đoạn nào cũng không cùng nằm trên một đường thẳng.
- Định nghĩa tứ giác lồi: Là tứ giác luôn nằm trong một nửa mặt phẳng có bờ là đường thẳng chứa bất kì cạnh nào của tứ giác.

∗ Chú ý: Từ nay, khi nói đến tứ giác mà không chú thích gì thêm, ta hiểu đó là tứ giác lồi.
2. Tổng các góc trong một tứ giác lồi
- Định lí: Tổng các góc trong một tứ giác bằng 360o.
- Mở rộng: Tổng bốn góc ngoài ở bốn đỉnh của tứ giác bằng 360o.
3. Các dạng toán thường gặp về tứ giác lồi
3.1. Dạng 1. Tính số đo góc trong tứ giác lồi
*Phương pháp giải:
Sử dụng định lí về tổng bốn góc trong một tứ giác bằng 360o.
Ví dụ minh hoạ: Cho tứ giác ABCD có
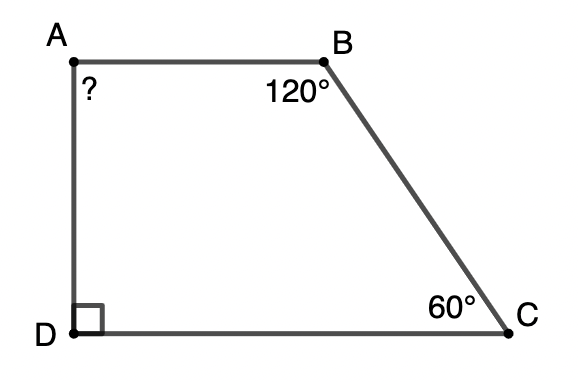
Lời giải:
Xét tứ giác ABCD có:
Vậy
Bài tập áp dụng
Cho tứ giác MNPQ có
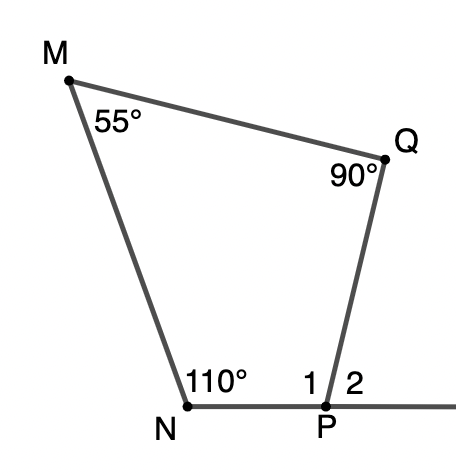
A. 75°
B. 105°
C. 55°
D. 110°
ĐÁP ÁN
Xét tứ giác MNPQ có:
Mà
Vậy góc ngoài đỉnh P bằng 75°.
Đáp án A.
3.2. Dạng 2: Bài toán liên quan giữa cạnh và đường chéo của tứ giác lồi
*Phương pháp giải:
Ta có thể chia tứ giác thành các tam giác, sau đó vận dụng bất đẳng thức tam giác.
Ví dụ 1: Tứ giác ABCD có hai đường chéo vuông góc với nhau, AB = 8cm, BC = 7cm, AD = 4cm. Tính độ dài đoạn CD.
Lời giải:
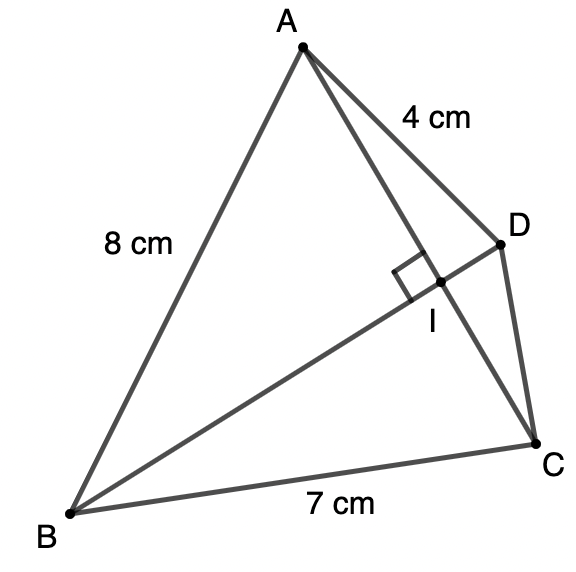
Gọi I là giao điểm của AC và BD.
Ta có: Xét ΔAID vuông tại I có: IA2 + ID2 = AD2 (Định lí Pytago)
Xét ΔBIC vuông tại I có: IB2 + IC2 = BC2 (Định lí Pytago)
Do đó: IA2 + ID2 + IB2 + IC2 = AD2 + BC2 = 42 + 72 = 65
Mà IA2 + IB2 = AB2 ; IC2 + ID2 = CD2 (Định lí Pytago)
⇒ IA2 + ID2 + IB2 + IC2 = (IA2 + IB2) + (IC2 + ID2) = AB2 + CD2
⇒ AB2 + CD2 = 65
⇒ 64 + CD2 = 65
⇒ CD2 = 1
⇒ CD = 1
Vậy CD = 1 (cm).
Ví dụ 2: Cho tứ giác ABCD. Chứng minh
Lời giải:
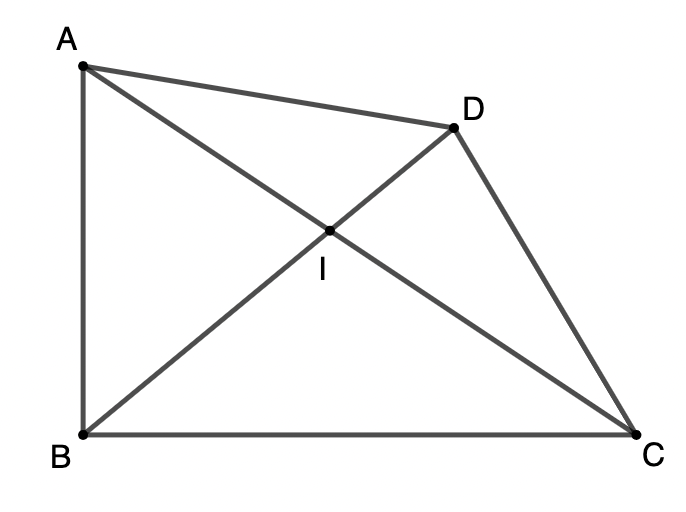
Gọi I là giao điểm của AC và BD. Theo bất đẳng thức tam giác ta có:
IA + IB > AB;
IB + IC > BC;
IC + ID > CD;
ID + IA > AD.
Cộng từng vế, ta được: IA + IB + IB + IC + IC + ID + ID + IA > AB + BC + CD + DA
⇒ 2(IA + IB + IC + ID) > AB + BC + CD + DA
⇒ 2[(IA + IB) + (IC + ID)] > p
⇒ 2(AC + BD) > p
⇒ AC + BD >
Bài tập áp dụng
Bài 1: Cho tứ giác MNPQ có hai đường chéo vuông góc với nhau tại O, biết rằng MO = 6cm, MN = 10cm, PQ = 5cm, OQ = 3cm. Tính độ dài NP.
A.
B.
C.
D.
ĐÁP ÁN
.png)
Ta có: Xét ΔMON vuông tại O có: OM2 + ON2 = MN2 (Định lí Pytago)
⇒ 62 + ON2 = 102
⇒ ON2 = 100 - 36
⇒ ON2 = 64
⇒ ON = 8 (cm)
Xét ΔQOP vuông tại O có: OQ2 + OP2 = QP2 (Định lí Pytago)
⇒ 32 + OP2 = 52
⇒ OP2 = 25 - 9
⇒ OP2 = 16
⇒ OP = 4 (cm)
Xét ΔNOP vuông tại O có: ON2 + OP2 = NP2 (Định lí Pytago)
⇒ 82 + 42 = NP2
⇒ NP2 = 80
Đáp án C.
Bài 2: Cho tứ giác ABCD. So sánh AC + BD và p với p là chu vi của tứ giác.
A. AC + BD = p
B. AC + BD > p
C. AC + BD < p
ĐÁP ÁN
.png)
Áp dụng bất đẳng thức tam giác vào hai tam giác ABC, ADC, ta có:
AC < AB + BC; AC < AD + DC
Cộng từng vế, ta được: AC + AC < AB + BC + AD + DC
Áp dụng bất đẳng thức tam giác vào hai tam giác ABD, CBD, ta có:
BD < AB + AD; BD < CB + CD
Cộng từng vế, ta được: BD + BD < AB + AD + CB + CD
Từ (1) và (2)
Đáp án C.
4. Một vài bài tập nâng cao phát triển tư duy về tứ giác lồi
Bài 1: Cho tứ giác ABCD biết
A. 10° ; 20° ; 30° ; 40°.
B. 36° ; 72° ; 108° ; 144°.
C. 30° ; 60° ; 90° ; 120°.
D. 40° ; 80° ; 120° ; 160°.
ĐÁP ÁN
Ta có:
Mà
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
Đáp án B.
Bài 2: Cho tứ giác ABCD, các tia phân giác của
ĐÁP ÁN
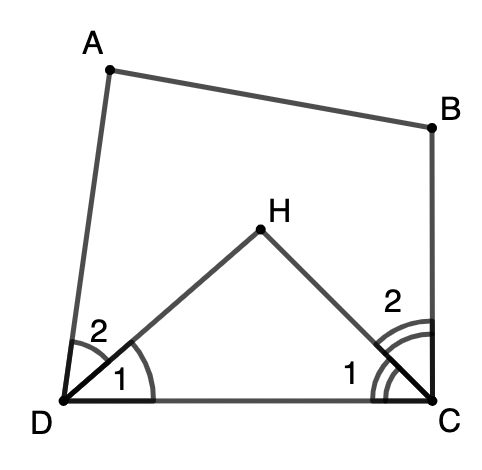
Xét ΔDHC có:
Mà
Xét tứ giác ABCD có:
Do đó:
Trên đây là tổng hợp kiến thức về tứ giác lồi và các bài toán gồm dạng cơ bản, dạng mở rộng. Nắm vững lý thuyết và luyện tập các bài toán trên sẽ giúp các em vận dụng tốt vào giải bài tập về tứ giác lồi.
Chịu trách nhiệm nội dung: GV Nguyễn Thị Trang
