
a) Vì ∆SAB cân tại S nên đường cao SH đồng thời là đường trung tuyến.
⇒ H là trung điểm của AB.
Áp dụng định lí Py-ta-go vào ∆SHA vuông tại H, ta có:
Diện tích xung quanh của hình chóp:
Diện tích đáy của hình chóp:
Diện tích toàn phần của hình chóp:

b) Vì ∆SCD cân tại S nên đường cao SH đồng thời là đường trung tuyến.
⇒ H là trung điểm của CD.
Áp dụng định lí Py-ta-go vào ∆SHD vuông tại H, ta có:
Diện tích xung quanh của hình chóp:
Vì đáy của hình chóp là lục giác đều ABCDEG nên ∆OCD là tam giác đều có đường cao OH.
Áp dụng định lí Py-ta-go vào ∆OHD vuông tại H, ta có:
Diện tích đáy của hình chóp bằng 6 lần diện tích của ∆OCD:
Diện tích toàn phần của hình chóp:

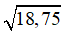 ≈ 4,33;
≈ 4,33;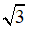 ≈ 1,73;
≈ 1,73; 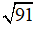 ≈ 9,54.
≈ 9,54.