Table of Contents
I. Định Nghĩa:
Hình bình hành là tứ giác có 2 cặp cạnh đối song song.
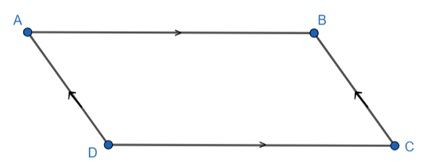
Hình bình hành ABCD có: AB // CD; AD // BC
II. Tính Chất:
Hình bình hành có:
+ Hai cặp cạnh đối song song.
+ Hai cặp cạnh đối bằng nhau.
+ Hai cặp góc đối bằng nhau.
+ Hai đường chéo cắt nhau tại trung điểm của mỗi đường.

Hình bình hành ABCD có:
AB // CD; AD // BC
AB = CD; AD = BC
O là trung điểm của AC và BD
III. Cách Chứng Minh:
1. Chứng minh tứ giác có 2 cặp cạnh đối song song.
2. Chứng minh tứ giác có 2 cặp cạnh đối bằng nhau.
3. Chứng minh tứ giác có 2 cặp góc đối bằng nhau.
4. Chứng minh tứ giác có 2 đường chéo cắt nhau tại trung điểm của mỗi đường.
5. Chứng minh tứ giác có 1 cặp cạnh đối vừa song song vừa bằng nhau.
Trong các tứ giác ở hình 70, tứ giác nào là hình bình hành? Vì sao?

a) Xét tứ giác ABCD, ta có:
AB = CD (gt)
AD = BC (gt)
=> Tứ giác ABCD là hình bình hành (Tứ giác có 2 cặp cạnh đối bằng nhau)
b) Xét tứ giác EFGH, ta có:
=> Tứ giác EFGH là hình bình hành (Tứ giác có 2 cặp góc đối bằng nhau)
c) Tứ giác INMK không phải là hình bình hành.
d) Xét tứ giác PSRQ, ta có:
O là trung điểm của SQ (gt)
O là trung điểm của PR (gt)
=> Tứ giác PSRQ là hình bình hành (Tứ giác có 2 đường chéo cắt nhau tại trung điểm của mỗi đường)
e) Ta có:
Mà 2 góc này ở vị trí trong cùng phía
Nên XV // UY
Xét tứ giác VXYU, ta có:
VX // UY (cmt)
VX = UY (gt)
=> Tứ giác VXYU là hình bình hành (Tứ giác có 1 cặp cạnh đối vừa song song vừa bằng nhau).
Biên soạn: GV. Lương Đình Trung
SĐT: 0916 872 125
Đơn Vị: Trung Tâm Đức Trí - 028 6654 0419
Địa chỉ: 26/5 đường số 4, KP 3, P. Bình Hưng Hòa A, Q. Bình Tân, TP.HCM
Fanpage: https://www.fb.com/ttductri
