Table of Contents
Trong bài học trước, ta đã được tìm hiểu về các tính chất thừa nhận qua việc nghiên cứu về hình học không gian. Một mặt phẳng hoàn toàn được xác nhận dựa vào các tính chất thừa nhận đã được học trong bài trước. Vậy có bao nhiêu cách xác định một mặt phẳng? Bài viết này VOH Giáo Dục sẽ nêu cho các bạn các cách xác định một mặt phẳng và trình bày một số dạng toán thường gặp liên quan đến phần kiến thức này.
1. Có bao nhiêu cách xác định một mặt phẳng?
Ta có 3 cách xác định một mặt phẳng như sau:
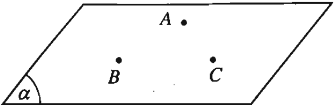
(1) Một mặt phẳng hoàn toàn được xác định khi biết mặt phẳng đó đi qua 3 điểm không thẳng hàng.
Cho 3 điểm A, B, C không thẳng hàng. Khi đó, từ 3 điểm A, B, C không thẳng hàng đã cho, ta hoàn toàn xác định một mặt phẳng, ký hiệu mặt phẳng đó là mp (ABC) hay (ABC).
(2) Một mặt phẳng hoàn toàn được xác định khi biết mặt phẳng đó đi qua một 1 và chứa 1 đường thẳng không đi qua điểm đó.
Cho đường thẳng d và điểm A không thuộc đường thẳng d. Khi đó, từ đường thẳng d và điểm A đã cho, ta hoàn toàn xác định một mặt phẳng, ký hiệu mặt phẳng đó là mp (A, d) hay (A, d), hoặc mp (d, A) hay (d, A).

(3) Một mặt phẳng hoàn toàn được xác định khi biết mặt phẳng đó chứa 2 đường thẳng cắt nhau.
Cho 2 đường thẳng a và b cắt nhau. Khi đó, từ 2 đường thẳng a và b đã cho, ta hoàn toàn xác định một mặt phẳng, ký hiệu mặt phẳng đó là mp (a, b) hay (a, b), hoặc mp (b, a) hay (b, a).

2. Các dạng toán thường gặp về xác định một mặt phẳng
Dạng 1: Xác định giao tuyến của 2 mặt phẳng
* Phương pháp giải:
Muốn tìm giao tuyến của 2 mặt phẳng bất kỳ nào đó, ta sẽ đi tìm 2 điểm chung của 2 mặt phẳng đó. Khi đó, đường thẳng đi qua 2 điểm chung vừa tìm được ở trên chính là giao tuyến của 2 mặt phẳng đã cho.
Cụ thể, ta tìm điểm chung của 2 mặt phẳng (α) và (β) như sau: Trên 2 mặt phẳng (α) và (β) ta xác định 2 đường thẳng a, b sao cho a thuộc (α), b thuộc (β) và chúng cùng nằm trong mặt phẳng (ϒ) nào đó. Khi đó, điểm chung của 2 mặt phẳng (α) và (β) chính là giao điểm A của 2 đường thẳng trên.

Bài tập vận dụng:
Bài 1. Cho 4 điểm M, N, P, Q không cùng nằm trong một mặt phẳng. Gọi H là trực tâm của tam giác NPQ. Giao tuyến của mặt phẳng (MPQ) và mặt phẳng (MNH) là gì?
- Đường thẳng MK, với K là chân đường vuông góc xuất phát từ đỉnh M của tam giác MNH.
- Đường thẳng ME, với E là trung điểm của đoạn thẳng PQ.
- Đường thẳng MF, với F là chân đường vuông góc xuất phát từ đỉnh N của tam giác NPQ.
- Đường thẳng MJ, với J là trọng tâm của tam giác MPQ.
ĐÁP ÁN

Ta có M thuộc mặt phẳng (MPQ) và mặt phẳng (MNH), nên M là điểm chung thứ nhất của mặt phẳng (MPQ) và mặt phẳng (MNH).
Gọi F là giao điểm của NH và PQ hay F là chân đường vuông góc xuất phát từ đỉnh N của tam giác NPQ, suy ra F
Mà NH
PQ
Do đó, F là điểm chung thứ hai của mặt phẳng (MPQ) và mặt phẳng (MNH).
Vậy MF là giao tuyến của mặt phẳng (MPQ) và mặt phẳng (MNH).
Chọn đáp án C.
Bài 2. Cho 4 điểm M, N, P, Q không cùng thuộc một mặt phẳng. Gọi E và F lần lượt là trung điểm của MQ và PQ. Giao tuyến của mặt phẳng (NEF) và mặt phẳng (MPQ) là gì?
- Đường thẳng NE.
- Đường thẳng PF.
- Đường thẳng QN.
- Đường thẳng EF.
ĐÁP ÁN

Ta có E và F cùng thuộc mặt phẳng (NEF). (1)
Do E và F lần lượt là trung điểm của MQ và PQ, suy ra E
Mà MQ
PQ
Do đó, E và F cùng thuộc mặt phẳng (MPQ). (2)
Từ (1) và (2), ta suy ra EF là giao tuyến của mặt phẳng (NEF) và mặt phẳng (MPQ).
Chọn đáp án D.
Bài 3. Cho tứ giác MNPQ, biết các cặp cạnh đối của tứ giác không song song với nhau và điểm E không thuộc mặt phẳng (MNPQ). Em hãy xác định giao tuyến của mặt phẳng (EMP) và mặt phẳng (ENQ).
ĐÁP ÁN

Ta có E
Trong mặt phẳng (MNPQ) gọi F là giao điểm của MP và NQ, suy ra F
Mà MP
NQ
Do đó, F là điểm chung thứ hai của mặt phẳng (EMP) và mặt phẳng (ENQ).
Vậy EF là giao tuyến của mặt phẳng (EMP) và mặt phẳng (ENQ).
Dạng 2: Tìm giao điểm của một đường thẳng và một mặt phẳng
* Phương pháp giải:
Muốn tìm giao điểm của một đường thẳng và một mặt phẳng, ta có những cách thực hiện sau;
+ Cách 1: Ta đưa về bài toán tìm giao điểm của đường thẳng đã cho với một đường thẳng nào đó nằm trong mặt phẳng đã cho.
+ Cách 2: Ta tìm một mặt phẳng nào đó chứa đường thẳng đã cho rồi xác định giao tuyến của 2 mặt phẳng đó, rồi ta tìm giao điểm của đường thẳng đã cho với giao tuyến vừa tìm được. Khi đó, giao điểm vừa tìm được chính là giao điểm của đường thẳng và mặt phẳng đã cho.
Bài tập vận dụng:
Bài 4. Cho tam giác MNP và điểm I không thuộc (MNP). Gọi E là một điểm bất kỳ nằm trên đoạn thẳng MP và H, K là hai điểm bất kỳ lần lượt nằm trên hai đoạn thẳng IM, IP. Em hãy tìm giao điểm của đường thẳng HK với mặt phẳng (IEN).
ĐÁP ÁN

Trong mặt phẳng (IMP), gọi F là giao điểm của IE và HK.
Khi đó F
F
Do đó, F là giao điểm của đường thẳng HK với mặt phẳng (IEN).
Bài 5. Cho 4 điểm M, N, P, Q không cùng nằm trong một mặt phẳng. Gọi I, J là hai điểm bất kỳ lần lượt nằm trên hai đoạn thẳng MN, MQ sao cho IJ không song song với NQ. Giao điểm của đường thẳng IJ với mặt phẳng (NPQ) là:
- Giao điểm của 2 đường thẳng IJ và MN.
- Giao điểm của 2 đường thẳng IJ và MQ.
- Giao điểm của 2 đường thẳng IJ và NQ.
- Giao điểm của 2 đường thẳng IJ và NP.
ĐÁP ÁN

Trong mặt phẳng (MNQ) ta có IJ không song song với NQ, nên gọi E là giao điểm của NQ và IJ.
Khi đó, E
E
Do đó, E là giao điểm của đường thẳng IJ với mặt phẳng (NPQ).
Chọn đáp án C.
Bài viết trên đã nêu cho các bạn các cách xác định một mặt phẳng và trình bày một số dạng toán thường gặp liên quan đến phần kiến thức này. Hy vọng qua đó các bạn sẽ tự tin hơn trong quá trình học và giải bài tập.
Chịu trách nhiệm nội dung: GV Nguyễn Thị Trang
