Table of Contents
Hình chóp tứ giác đều là một nội dung quan trọng trong chương trình môn toán lớp 11. Vậy, hình chóp tứ giác đều là hình như thế nào? Các vấn đề trọng tâm về hình chóp tứ giác đều là gì? Chúng ta có thể vận dụng kiến thức được học vào xử lí các bài tập về hình chóp tứ giác đều ra sao? Đó chính là những nội dung sẽ lần lượt được đề cập trong bài viết sau đây.
1. Hình chóp tứ giác đều là gì ?
+ Hình chóp tứ giác đều là hình chóp có mặt đáy là hình vuông, các mặt bên là những tam giác cân bằng nhau có chung đỉnh
Ví dụ: Hình chóp đều S.ABCD có:
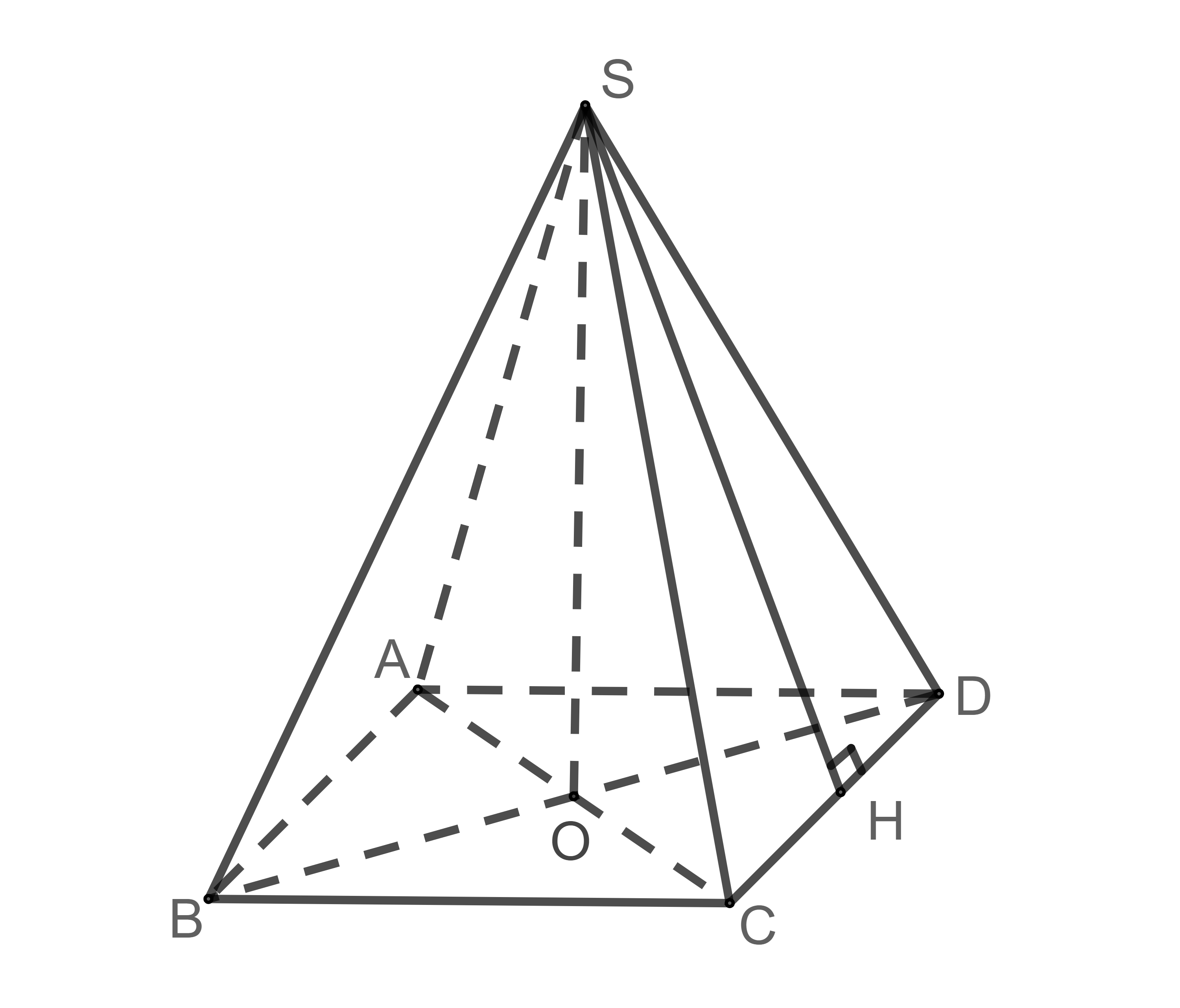
+ SO là đường cao hay còn gọi là chiều cao (là đoạn nối từ đỉnh tới tâm của đáy)
+ SH là trung đoạn (là đường cao hạ từ đỉnh S của mỗi mặt bên)
+ Đáy ABCD là hình vuông
+ Các mặt bên là những tam giác cân bằng nhau
2. Các vấn đề trọng tâm về hình chóp tứ giác đều
2.1. Diện tích xung quanh hình chóp tứ giác đều
+ Công thức tính diện tích xung quanh của hình chóp tứ giác đều
Sxq = p.d
Trong đó: p là nửa chu vi đáy; d là trung đoạn
Ví dụ: Hình chóp tứ giác đều S.ABCD có độ dài một cạnh đáy là 3 cm, độ dài trung đoạn bằng 5 cm. Tính diện tích xung quanh của hình chóp tứ giác đều?
Giải
Diện tích xung quanh của hình chóp tứ giác đều là:
Sxq = p.d = 3.2.5 = 30 (cm2)
2.2. Diện tích toàn phần hình chóp tứ giác đều
+ Công thức tính diện tích toàn phần của hình chóp tứ giác đều
Stp = Sxq + Sđáy
Ví dụ: Hình chóp tứ giác đều S.ABCD có độ dài một cạnh đáy là 3 cm, độ dài trung đoạn bằng 5 cm. Tính diện tích toàn phần của hình chóp tứ giác đều?
Giải
Diện tích toàn phần của hình chóp tứ giác đều là:
Stp = Sxq + Sđáy = 30 + 3.3 = 39 (cm2)
2.3. Thể tích hình chóp tứ giác đều
+ Công thức tính thể tích của hình chóp tứ giác đều
V =
Trong đó: S là diện tích đáy; h là chiều cao
Ví dụ: Hình chóp tứ giác đều S.ABCD có độ dài một cạnh đáy là 3 cm, độ dài trung đoạn bằng 5 cm. Tính diện thể tích của hình chóp tứ giác đều?
Giải

Theo đề bài, ta có: SH = 5 cm; BC = 3 cm
Mà OH = BC:2 = 3:2 = 1,5 cm
Áp dụng định lí Py-ta-go vào tam giác SOH vuông tại O có:
SO2 + OH2 = SH2
Suy ra: SO2 = SH2 - OH2 = 52 - 1,52 = 22,75
Vậy, SO =
Thể tích hình chóp tứ giác đều S.ABCD là:
V =
2.4. Xác định giao tuyến của các mặt phẳng trong hình chóp tứ giác đều
+ Giao tuyến của hai mặt phẳng là đường thẳng chứa tất cả các điểm chung của hai mặt phẳng đó
Ví dụ: Cho hình chóp tứ giác đều S.ABCD. Tìm giao tuyến của hai mặt phẳng (SAB) và (ABCD)
Giải

Vì A và B lần lượt là hai điểm chung của hai mặt phẳng (SAB) và (ABCD) nên giao tuyến của hai mặt phẳng (SAB) và (ABCD) là đường thẳng AB
Vậy, (SAB)
2.5. Hình chóp tứ giác đều có bao nhiêu mặt phẳng đối xứng ?
Cho hình chóp tứ giác đều S.ABCD. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA.
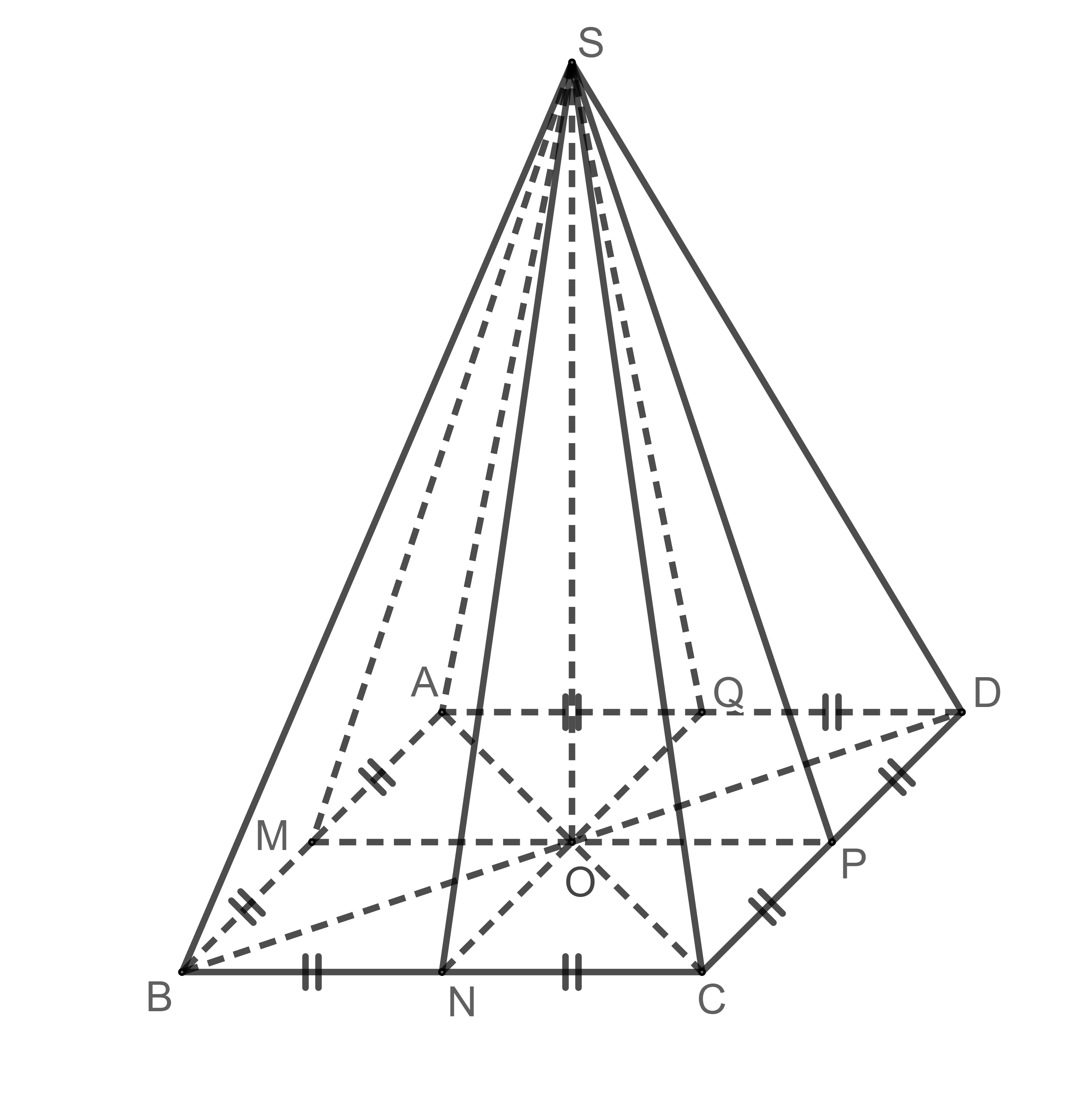
Khi đó, ta có: Số mặt phẳng đối xứng của hình chóp tứ giác đều S.ABCD là 4 mặt phẳng. Đó là các mặt phẳng: (SAC), (SBD), (SMP), (SNQ)
3. Bài tập ứng dụng về hình chóp tứ giác đều
Bài 1: Thể tích của hình chóp tứ giác đều thay đổi như thế nào khi độ dài cạnh đáy gấp lên 5 lần?
- Thể tích gấp lên 5 lần
- Thể tích giảm xuống 5 lần
- Thể tích gấp lên 25 lần
- Thể tích giảm xuống 25 lần
ĐÁP ÁN
Vì độ dài cạnh đáy gấp lên 5 lần nên diện tích đáy gấp lên 5.5 = 25 lần
Do đó, thể tích gấp lên 25 lần
Chọn câu C
Bài 2: Cho hình chóp tứ giác đều S.ABCD.

Hãy cho biết giao tuyến của hai mặt phẳng (SAC) và (SBD) là:
- Điểm S
- Đường thẳng AC
- Đường thẳng BD
- Đường thẳng SO
ĐÁP ÁN
+ Ta có: O là giao điểm của hai đường chéo AC và BD
Do đó, O
Vậy, O
+ Mặt khác, S
Vậy, giao tuyến của hai mặt phẳng (SAC) và (SBD) là đường thẳng SO
Chọn câu D
Bài 3: Hình chóp tứ giác đều có diện tích toàn phần là 253 cm2, trung đoạn có độ dài là 6 cm. Lúc này, độ dài một cạnh của mặt đáy là:
- 10 cm
- 11 cm
- 12 cm
- Chưa thể kết luận
ĐÁP ÁN
Ta có: Stp = Sxq + Sđáy
Gọi a (cm) (a > 0) là độ dài một cạnh của đáy ta có:
Stp = 2.a.d + a2 = 2.a.6 + a2 = 12.a + a2
Vì Stp = 253 cm2 nên 12.a + a2 = 253
Hay a2 + 12.a - 253 = 0
Giải phương trình bậc hai này ta thu được: a = 11 (thỏa mãn) và a = - 23 (loại)
Vậy, độ dài một cạnh của mặt đáy là 11 cm
Chọn câu B
Bài 4: Số trung đoạn trong một hình chóp tứ giác đều là:
- 1
- 2
- 3
- 4
ĐÁP ÁN
Trung đoạn là đường cao hạ từ đỉnh của mỗi mặt bên.
Vì hình chóp tứ giác đều có 4 mặt bên nên sẽ có 4 trung đoạn
Chọn câu D
Bài 5: Trong các phát biểu sau đây, phát biểu đúng là:
- Diện tích toàn phần của một hình chóp tứ giác đều là 110 cm2, khi độ dài cạnh đáy tăng gấp 3 lần thì diện tích toàn phần mới là 330 cm2
- Diện tích toàn phần của một hình chóp tứ giác đều là 110 cm2, khi độ dài cạnh đáy tăng gấp 3 lần thì diện tích toàn phần mới nhỏ hơn 330 cm2
- Diện tích toàn phần của một hình chóp tứ giác đều là 110 cm2, khi độ dài cạnh đáy tăng gấp 3 lần thì diện tích toàn phần mới lớn hơn 330 cm2
- Diện tích toàn phần của một hình chóp tứ giác đều là 110 cm2, khi độ dài cạnh đáy tăng gấp 3 lần thì diện tích toàn phần mới không thay đổi
ĐÁP ÁN
Gọi a là độ dài cạnh đáy; d là độ dài trung đoạn
Diện tích toàn phần lúc đầu là:
Stp = 2.a.d + a2
Diện tích toàn phần lúc sau là:
S'tp = 2.3a.d + (3a)2 = 6.a.d + 9a2 = 3.(2.a.d + 3a2)
Vì 2.a.d + 3a2 > 2.a.d + a2
Nên S'tp > 3.110 = 330 cm2
Chọn câu C
Thông qua bài viết, mong rằng các em có thể ghi nhớ các vấn đề trọng tâm về hình chóp tứ giác đều đồng thời có thể vận dụng giải quyết nhiều bài tập hơn nữa.
Chịu trách nhiệm nội dung: GV Nguyễn Thị Trang
