Table of Contents
Trong chuyên đề trước, ta đã được học về hình chóp đa giác lồi và biết được hình chóp đa giác lồi có bao nhiêu mặt. Vậy hình chóp tứ giác là gì? Hình chóp tứ giác có bao nhiêu mặt? Bài viết sẽ nhắc lại cho các bạn khái niệm về hình chóp đa giác lồi và giải đáp câu hỏi: Hình chóp tứ giác có bao nhiêu mặt? Cùng VOH Giáo Dục theo dõi bài viết dưới đây nhé các bạn.
1. Nhắc lại khái niệm về hình chóp
Trong mặt phẳng (α), cho một đa giác lồi X1 X2 ... Xn có n cạnh. Lấy một điểm S không nằm trong mặt phẳng (α). Nối điểm S lần lượt với các đỉnh X1 , X2 , ... , Xn ta thu được n tam giác SX1X2 , SX2X3 , ... , SXnX1. Hình gồm đa giác lồi X1 X2 ... Xn và n tam giác SX1X2 , SX2X3 , ... , SXnX1 được gọi là hình chóp, ký hiệu là S.X1X2...Xn. Khi đó hình chóp này có tất cả n + 1 mặt. Ta gọi điểm S là đỉnh, đa giác X1X2...Xn là mặt đáy. Các tam giác SX1X2 , SX2X3 , ... , SXnX1 được gọi là các mặt bên; các đoạn thẳng SX1 , SX2 , ... , SXn được gọi là các cạnh bên, các cạnh của đa giác đáy X1X2 , X2X3 , ... , XnX1 được gọi là các cạnh đáy của hình chóp.
Chú ý: Hình chóp có đáy là tam giác, tứ giác, ngũ giác, lục giác, ... được gọi lần lượt là hình chóp tam giác, hình chóp tứ giác, hình chóp ngũ giác, hình chóp lục giác, ...
2. Hình chóp tứ giác có bao nhiêu mặt?
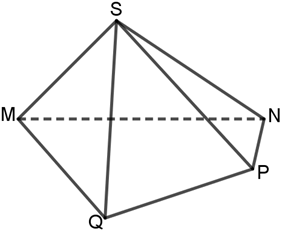
Trong mặt phẳng (α), cho tứ giác MNPQ. Lấy một điểm S không nằm trong mặt phẳng (α). Nối điểm S lần lượt với các đỉnh M, N, P, Q ta thu được 4 tam giác SMN, SNP, SPQ, SQM. Hình gồm tứ giác MNPQ và 4 tam giác SMN, SNP, SPQ, SQM được gọi là hình chóp tứ giác, ký hiệu là S.MNPQ. Khi đó hình chóp tứ giác này có tất cả 4 + 1 = 5 mặt.
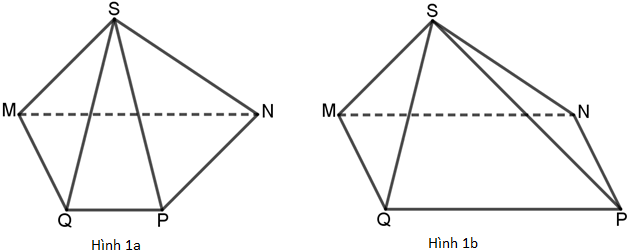
Ví dụ 1. Một số hình chóp tứ giác thường gặp:
+ Hình chóp S.MNPQ có đáy là hình thang MNPQ (Hình 1a).
+ Hình chóp S.MNPQ có đáy là hình bình hành MNPQ (Hình 1b).
3. Một số dạng bài tập về hình chóp tứ giác
Bài 1. Em hãy điền những từ, cụm từ thích hợp còn thiếu vào mỗi chỗ trống trong các câu sau đây:
1) Hình chóp đa giác lồi S.X1 X2 ... Xn có tất cả ___ mặt;
2) Hình chóp tam giác S.HKT có tất cả ___ mặt;
3) Hình chóp ___ có tất cả 5 mặt;
4) Hình chóp ___ có tất cả 7 mặt.
ĐÁP ÁN
Hình chóp đa giác lồi S.X1 X2 ... Xn là hình gồm đa giác lồi X1 X2 ... Xn và n tam giác SX1X2 , SX2X3 , ... , SXnX1, nên suy ra hình chóp này có tất cả n + 1 mặt.
Tương tự, ta có:
+ Hình chóp tam giác S.HKT có tất cả 3 + 1 = 4 mặt.
+ Hình chóp có tất cả 5 mặt, nên suy ra hình chóp đó có 5 – 1 = 4 mặt bên, hay hình chóp đó có đáy là tứ giác.
+ Hình chóp có tất cả 7 mặt, nên suy ra hình chóp đó có 7 – 1 = 6 mặt bên, hay hình chóp đó có đáy là lục giác.
Khi đó, ta điền từ còn thiếu vào các câu đã cho như sau:
1) Hình chóp đa giác lồi S.X1 X2 ... Xn có tất cả n + 1 mặt;
2) Hình chóp tam giác S.HKT có tất cả 4 mặt;
3) Hình chóp tứ giác có tất cả 5 mặt;
4) Hình chóp lục giác có tất cả 7 mặt.
Bài 2. Cho hình chóp tứ giác S.HKEF có đáy HKEF là hình thang (HK // EF và EF < HK). Giao tuyến của 2 mặt phẳng (SHF) và (SKE) là:
- đường thẳng SO (với O = HE
KF). - đường thẳng SE.
- đường thẳng SF.
- đường thẳng SX (với X = HF
KE).
ĐÁP ÁN

Vì S thuộc hai mặt phẳng (SHF) và (SKE), suy ra S
Trong mp (HKEF), gọi X = HF
X
X
Khi đó, ta được X
Từ (1) và (2), ta suy ra SX = (SHF)
Đáp án đúng là D.
Bài 3. Cho hình chóp tứ giác S.HKEF có đáy HKEF là hình thang (HK // EF và EF < HK). Gọi 2 điểm M, N lần lượt là trung điểm của SH, SK. Gọi điểm P là giao điểm của HE và KF. Giao tuyến của 2 mặt phẳng (EMN) và (SFK) là:
- đường thẳng SP.
- đường thẳng NQ (với Q = ME
SP). - đường thẳng FQ (với Q = ME
SP). - đường thẳng KQ (với Q = ME
SP).
ĐÁP ÁN
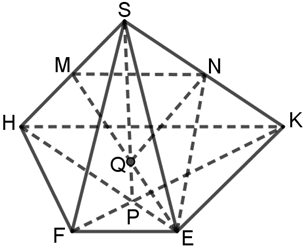
Vì N là trung điểm của SK, ta có:
N
N
Khi đó, ta được N = (EMN)
Trong mp (SHE), gọi Q = ME
Q
Q
Khi đó, ta được Q
Từ (1) và (2), ta suy ra NQ = (EMN)
Đáp án đúng là B.
Bài 4. Cho hình chóp tứ giác S.HKEF có đáy HKEF là hình bình hành. Gọi điểm A là một điểm bất kỳ nằm trên đoạn thẳng EF (A khác E, F). Em hãy xác định giao tuyến của 2 mặt phẳng (SAH) và (SKE).
ĐÁP ÁN
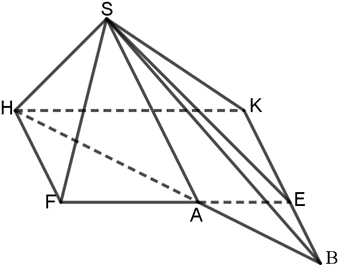
Vì S thuộc hai mặt phẳng (SAH) và (SKE), suy ra S
Trong mp (HKEF) có HF // KE và A là một điểm bất kỳ nằm trên đoạn thẳng EF (A khác E, F) nên HA cắt KE.
Gọi B = HA
B
B
Khi đó, ta được B
Từ (1) và (2), ta suy ra SB = (SAH)
Do đó, SB là giao tuyến của 2 mặt phẳng (SAH) và (SKE).
Bài 5. Cho hình chóp tứ giác S.HKEF có đáy HKEF là hình thang (HK // EF và EF < HK). Gọi X là trung điểm của đoạn thẳng KE. Hãy xác định giao tuyến của 2 mặt phẳng (SXF) và (SHE).
ĐÁP ÁN
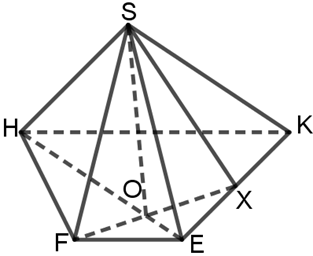
Vì S thuộc hai mặt phẳng (SXF) và (SHE), suy ra S
Trong mp (HKEF), gọi O = XF
O
O
Khi đó, ta được O
Từ (1) và (2), ta suy ra SO = (SXF)
Do đó, SO là giao tuyến của 2 mặt phẳng (SXF) và (SHE).
Bài viết đã nhắc lại cho các bạn khái niệm về hình chóp đa giác lồi và giải đáp câu hỏi: Hình chóp tứ giác có bao nhiêu mặt? Đồng thời bài viết cũng tổng hợp một số dạng bài tập liên quan đến hình chóp tứ giác, cảm ơn các bạn đã theo dõi bài viết này.
Chịu trách nhiệm nội dung: GV Nguyễn Thị Trang
