Hình chóp đều là gì? Tính chất và thể tích hình chóp đều

Hình chóp đều là một khối hình ba chiều có cạnh đáy là một đa giác đều và các cạnh đỉnh cùng dài và góc giữa hai cạnh là như nhau. Hình chóp đều thường có tính đối xứng và được sử dụng trong nhiều bài toán hình học và không gian từ cơ bản đến nâng cao. Cùng VOH Giáo dục ôn lại tổng quan kiến thức và thực hành một số bài tập liên quan về dạng hình chóp đều này nhé!

1. Nhắc lại hình chóp

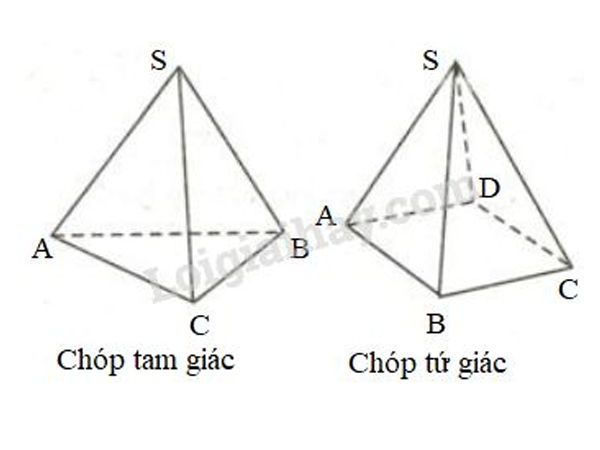
Hình chóp có đáy là một đa giác và các mặt bên là những tam giác có chung một đỉnh. Đỉnh này gọi là đỉnh của hình chóp

Đường cao của hình chóp là đường thẳng đi qua đỉnh và vuông góc với mặt phẳng đáy.

Hình chóp có đáy là tam giác gọi là hình chóp tam giác

Hình chóp có đáy là tứ giác được gọi là hình chóp tứ giác.

Công thức tính thể tích:

Trong đó: B là diện tích đáy. h là chiều cao của hình chóp (khoảng cách từ đỉnh đến mặt đáy)

2. Thế nào là hình chóp đều?

Định nghĩa hình chóp đều là hình chóp có mặt đáy là một đa giác đều (tam giác đều, hình vuông,...), có mặt bên là các tam giác cân bằng nhau và có chung đỉnh.

3. Tính chất hình chóp đều

Chân đường cao của hình chóp đa giác đều là tâm của mặt đáy.

Đường cao được vẽ từ đỉnh của mỗi mặt bên của hình chóp đều gọi là trung đoạn của hình chóp đó.

4. Thể tích hình chóp đều

Thể tích hình chóp đều được tính như sau:

Trong đó: S là diện tích đáy và h là chiều cao

Hình chóp tứ giác đều có các tính chất sau:

• Đáy là hình vuông
• Các cạnh bên bằng nhau
• Tất cả các mặt bên là các tam giác cân bằng nhau
• Chân đường cao trùng với tâm mặt đáy (tâm đáy là giao điểm 2 đường chéo)
• Tất cả các góc tạo bởi cạnh bên và mặt đáy bằng nhau

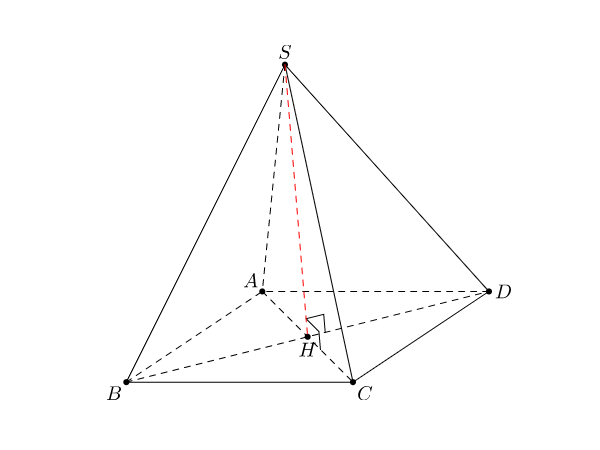
Thể tích hình chóp tứ giác đều:

Trong đó:

S.ABCD là diện tích đáy tứ giác đều ABCD

SH là chiều cao của hình chóp.

Hình chóp tam giác đều có các tính chất như sau:

• Hình chóp tam giác đều có 3 mặt phẳng đối xứng
• Đáy là tam giác đều
• Các cạnh bên bằng nhau
• Tất cả các mặt bên là các tam giác cân bằng nhau
• Chân đường cao trùng với tâm mặt đáy (tâm đáy là trọng tâm của tam giác)
• Tất cả các góc tạo bởi các mặt bên và mặt đáy đều bằng nhau
• Tất cả các góc tạo bởi cạnh bên và mặt đáy đều bằng nhau

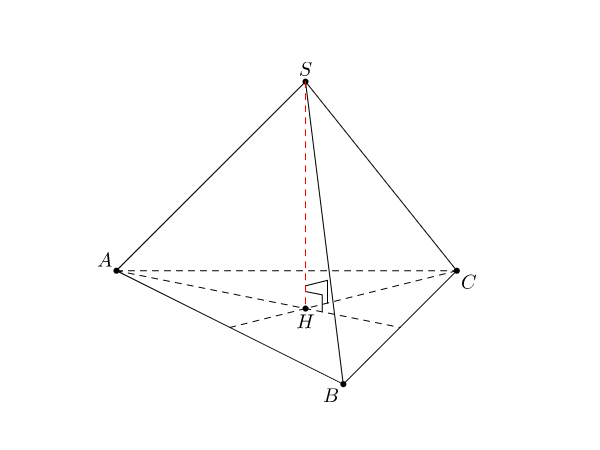
Thể tích hình chóp tam giác đều:

Trong đó:

S.ABC là diện tích đáy tam giác đều ABC

SH là chiều cao của hình chóp.

» Xem thêm: Công thức tính thể tích hình chóp đều chi tiết nhất

5. Hình chóp cụt đều

Cắt hình chóp đều bằng một mặt phẳng song song với đáy. Phần hình chóp nằm giữa mặt phẳng đó và mặt phẳng đáy của hình chóp là một hình chóp cụt đều

Tính chất của hình chóp cụt đều là:

• Mỗi mặt bên của hình chóp cụt đều là một hình thang cân.
• Hình chóp cụt đều có 2 mặt đáy
• Các mặt đáy song song với nhau

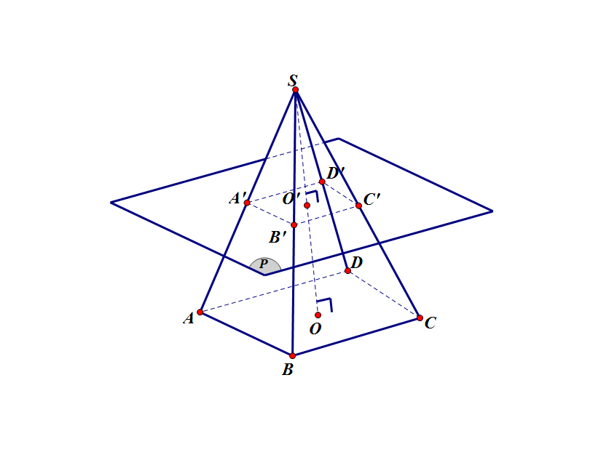
Thể tích hình chóp cụt:

Trong đó:

B, B' là diện tích của đáy lớn và đáy nhỏ của hình chóp cụt

h là chiều cao (khoảng cách giữa hai mặt phẳng chứa hai đáy)

6. Các dạng toán thông dụng về hình chóp đều

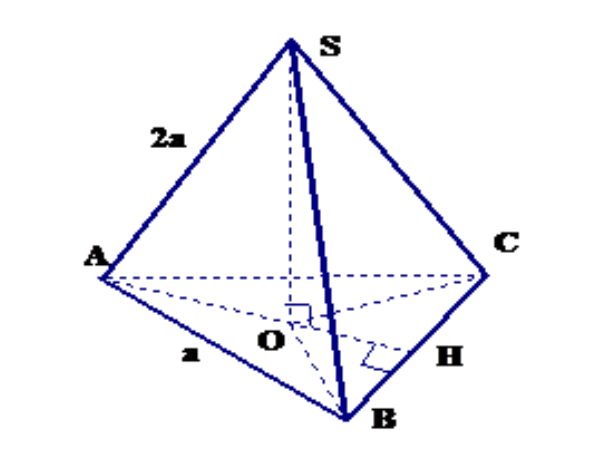
Bài tập 1:

Cho hình chóp tam giác đều S.ABC cạnh đáy bằng a, cạnh bên bằng 2a. Yêu cầu: Chứng minh chân đường cao kẻ từ S của hình chóp là tâm của tam giác đều ABC và tính thể tích hình chóp S.ABC.

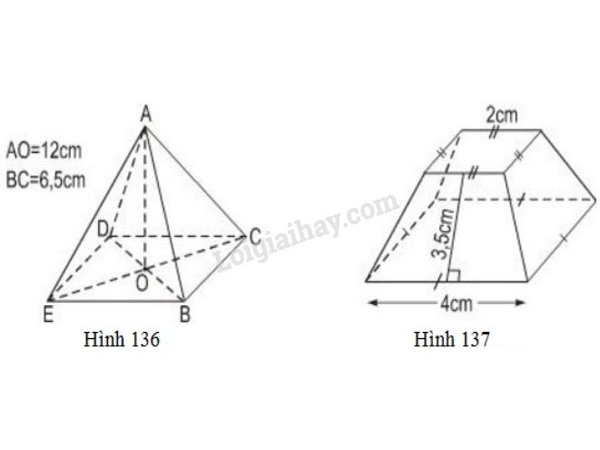
Bài tập 2: Yêu cầu:

a. Tính thể tích của hình chóp đều (h.136)

b. Tính diện tích xung quanh hình chóp cụt đều (h.137)

Bên trên là những kiến thức cơ bản nhất về hình chóp đều và một số bài tập ví dụ. Hy vọng qua bài viết các em học sinh sẽ nắm vững kiến thức và tính chất hình chóp đều để có thể áp dụng vào bài tập một cách hiệu quả nhất.