Table of Contents
Chúng ta đã được học về khái niệm hai điểm đối xứng qua một đường thẳng và hai hình đối xứng qua một đường thẳng trong các chuyên đề trước. Bài viết dưới đây sẽ giúp các bạn tìm hiểu về khái niệm hình có trục đối xứng ở Toán 8, cùng với đó bài viết sẽ chia sẻ cho các bạn một số dạng hình đã học mà chúng có trục đối xứng và tổng hợp một số bài tập bổ ích về chuyên đề này. Mời các bạn cùng tìm hiểu.
1. Hình có trục đối xứng là gì?
Định nghĩa tổng quát về hình có trục đối xứng: Cho hình H, khi đó ta nói hình H có trục đối xứng là đường thẳng d nếu điểm đối xứng với mỗi điểm thuộc hình H qua đường thẳng d cũng đều thuộc hình H.
Ta có thể nói rằng đường thẳng d là trục đối xứng của hình H trong trường hợp này.
» Xem thêm: Trục đối xứng là gì? Hình nào có trục đối xứng?
2. Các hình có trục đối xứng lớp 8
2.1. Tam giác cân
Cho tam giác OPQ cân tại O có đường cao OH. Ta có điểm đối xứng với mỗi điểm thuộc các cạnh của tam giác cân OPQ qua đường cao OH cũng đều thuộc các cạnh của tam giác cân OPQ. Khi đó, ta nói rằng tam giác cân OPQ có trục đối xứng là đường thẳng OH.

2.2. Tam giác đều
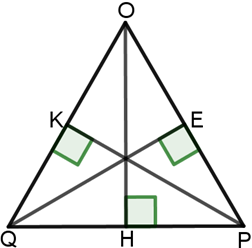
Cho tam giác đều OPQ có 3 đường cao OH, PK, QE. Ta có điểm đối xứng với mỗi điểm thuộc các cạnh của tam giác đều OPQ qua một trong 3 đường cao OH, PK, QE cũng đều thuộc các cạnh của tam giác đều OPQ. Khi đó, ta nói rằng tam giác đều OPQ có 3 trục đối xứng là 3 đường thẳng OH, PK, QE.
2.3. Hình thang cân
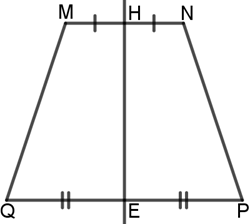
Cho hình thang cân MNPQ với MN // PQ có H và E lần lượt là trung điểm của 2 cạnh đáy MN và PQ. Ta có điểm đối xứng với mỗi điểm thuộc các cạnh của hình thang cân MNPQ qua đường thẳng HE cũng đều thuộc các cạnh của hình thang cân MNPQ. Khi đó, ta nói rằng hình thang cân MNPQ có trục đối xứng là đường thẳng HE.
3. Bài tập về hình có trục đối xứng lớp 8
Bài 1. Cho tam giác đều OPQ có 3 đường cao OH, PK, QE trong hình vẽ dưới đây. Em hãy chỉ ra đáp án sai trong các đáp án sau:

- 2 điểm K và H đối xứng với nhau qua đường thẳng QE.
- 2 đoạn thẳng QH và PH đối xứng với nhau qua đường thẳng OH.
- 2 góc KQH và KOE đối xứng với nhau qua đường thẳng KP.
- 2 điểm O và H đối xứng với nhau qua đường thẳng QE.
ĐÁP ÁN
Vì tam giác đều OPQ có 3 trục đối xứng là 3 đường thẳng OH, PK, QE, mà đường thẳng QE không phải là đường trung trực của đoạn thẳng nối 2 điểm O và H. Do đó 2 điểm O và H đối xứng với nhau qua đường thẳng QE là sai.
Chọn đáp án D.
Bài 2. Cho hình thang cân MNPQ với MN // PQ có H và E lần lượt là trung điểm của 2 cạnh đáy MN và PQ trong hình vẽ dưới đây. Em hãy điền các từ còn thiếu hợp lý vào mỗi câu sau:

1) Hai điểm M và N đối xứng với nhau qua đường thẳng . . .;
2) Hai góc MQE và . . . đối xứng với nhau qua đường thẳng HE;
3) Hai đoạn thẳng . . . và EP đối xứng với nhau qua đường thẳng HE;
4) Hai điểm . . . và P đối xứng với nhau qua đường thẳng HE.
ĐÁP ÁN
Vì hình thang cân MNPQ có trục đối xứng là đường thẳng HE, khi đó:
1) Hai điểm M và N đối xứng với nhau qua đường thẳng HE;
2) Hai góc MQE và NPE đối xứng với nhau qua đường thẳng HE;
3) Hai đoạn thẳng EQ và EP đối xứng với nhau qua đường thẳng HE;
4) Hai điểm Q và P đối xứng với nhau qua đường thẳng HE.
Bài 3. Cho lục giác đều MNPQRT. Khi đó lục giác đều MNPQRT có trục đối xứng không? Lục giác đều MNPQRT có tất cả bao nhiêu trục đối xứng?
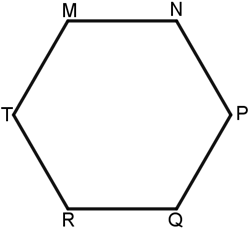
- Lục giác đều MNPQRT có trục đối xứng và có tất cả 3 trục đối xứng.
- Lục giác đều MNPQRT không có trục đối xứng.
- Lục giác đều MNPQRT có trục đối xứng và có tất cả 6 trục đối xứng.
- Lục giác đều MNPQRT có trục đối xứng và có tất cả 9 trục đối xứng.
ĐÁP ÁN

Ta có 3 đường thẳng MQ, NR, PT chính là 3 trục đối xứng của lục giác đều MNPQRT, vì điểm đối xứng với mỗi điểm thuộc các cạnh của lục giác đều MNPQRT qua một trong 3 đường thẳng MQ, NR, PT cũng đều thuộc các cạnh của lục giác đều MNPQRT.
Ta kẻ 3 đường trung trực của 3 đoạn thẳng MN, NP, PQ. Khi đó 3 đường trung trực của 3 đoạn thẳng MN, NP, PQ chính là 3 trục đối xứng của lục giác đều MNPQRT, vì điểm đối xứng với mỗi điểm thuộc các cạnh của lục giác đều MNPQRT qua một trong 3 đường trung trực của 3 đoạn thẳng MN, NP, PQ cũng đều thuộc các cạnh của lục giác đều MNPQRT.
Suy ra lục giác đều MNPQRT có trục đối xứng và có tất cả 6 trục đối xứng.
Chọn đáp án C.
Bài 4. Cho đường tròn tâm I. Khi đó đường tròn tâm I có trục đối xứng không? Đường tròn tâm I có tất cả bao nhiêu trục đối xứng?

- Đường tròn tâm I có trục đối xứng và có tất cả 1 trục đối xứng.
- Đường tròn tâm I có trục đối xứng và có tất cả 2 trục đối xứng.
- Đường tròn tâm I có trục đối xứng và có vô số trục đối xứng.
- Đường tròn tâm I không có trục đối xứng.
ĐÁP ÁN

Vì bất kỳ đường kính nào của đường tròn tâm I cũng chính là trục đối xứng của đường tròn tân I. Mà một đường tròn có vô số đường kính, do đó đường tròn tâm I có trục đối xứng và có vô số trục đối xứng.
Chọn đáp án C.
Bài 5. Em hãy kể tên 3 chữ cái in hoa khác nhau có trục đối xứng. Mỗi chữ in hoa đó có bao nhiêu trục đối xứng?
ĐÁP ÁN
3 chữ cái in hoa khác nhau có trục đối xứng là: X, Y, V. Ta có:
+ Chữ cái in hoa X có 2 trục đối xứng.
+ Chữ cái in hoa Y có 1 trục đối xứng.
+ Chữ cái in hoa V có 1 trục đối xứng.
Dưới đây là 3 hình vẽ minh họa cho 3 chữ cái in hoa khác nhau có trục đối xứng X, Y, V:

Kết luận: VOH Giáo Dục đã giới thiệu khái niệm hình có trục đối xứng toán 8, cùng với đó bài viết đã chia sẻ cho các bạn một số dạng hình đã học mà chúng có trục đối xứng. Hy vọng các bạn nắm rõ phần kiến thức này kết hợp làm tốt các bài toán trên lớp.
Chịu trách nhiệm nội dung: GV Nguyễn Thị Trang
