Góc đồng vị là gì? Hai góc đồng vị có bằng nhau không?

Trong các loại góc tạo thành từ một đường thẳng cắt hai đường thì góc đồng vị là loại góc tương đối dễ nhận biết. Vậy thế nào là góc đồng vị? Góc đồng vị có tính chất gì? Để giải đáp thắc mắc này thì chúng ta cùng VOH Giáo Dục tìm hiểu qua bài viết sau đây nhé.

1. Góc đồng vị là gì?

- Cho đường thẳng t cắt hai đường thẳng f và r lần lượt tại P và D như hình sau:

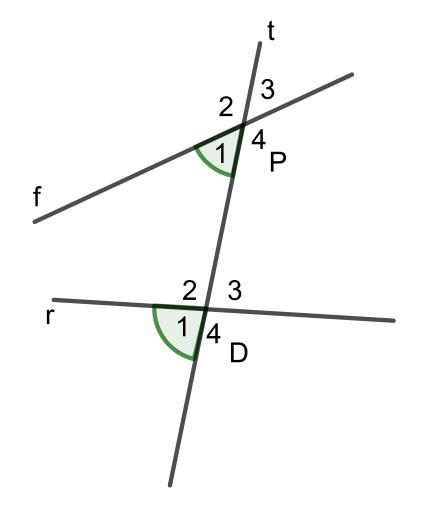
Khi đó: 

Hai góc P₁ và D₁ được gọi là hai góc đồng vị

Ta có thể hiểu hai góc đồng vị là hai góc nằm ở vị trí giống nhau.

*Nhận xét: Như vậy, đường thẳng t cắt hai đường thẳng f và r sẽ tạo ra bốn cặp góc đồng vị.

2. Tính chất của góc đồng vị

Nếu đường thẳng t cắt hai đường thẳng f và r và trong các góc tạo thành có một cặp góc đồng vị bằng nhau thì các cặp góc đồng vị khác cũng bằng nhau

3. Phương pháp nhận biết hai góc đồng vị

Để nhận biết hai góc đồng vị, ta dựa vào những dấu hiệu sau:

Cho đường thẳng t cắt hai đường thẳng u và v tạo thành các góc. Khi đó các cặp góc đồng vị có những đặc điểm sau:

- Hai góc không được chung gốc

- Hai góc đó phải nằm cùng một phía so với đường thẳng t và nằm ở vị trí giống nhau trên hai đường thẳng u và v

Ví dụ minh họa: 

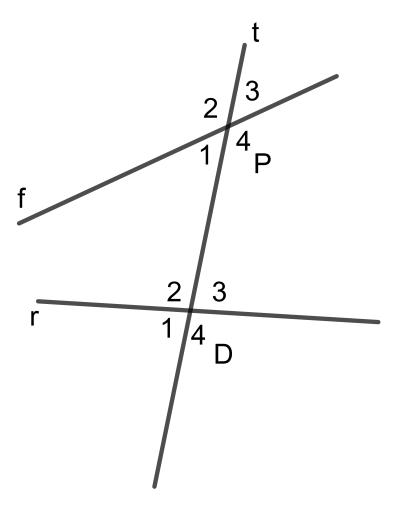
Quan sát hình vẽ trên, ta thấy các góc P₁, P₂, D₁, D₂ là các góc nằm ở phía bên trái so với đường thẳng t.

Các góc P₁ và D₁ không chung gốc và nằm ở vị trí giống nhau trên hai đường thẳng f và r nên hai góc  P₁ và D₁ là một cặp góc đồng vị. 

Các góc P₂ và D₂ không chung gốc và nằm ở vị trí giống nhau trên hai đường thẳng f và r nên hai góc  P₂ và D₂ là một cặp góc đồng vị. 

Tương tự như vậy ta cũng xác định được các cặp cặp góc P₃ và D₃, P₄ và D₄ là các cặp góc đồng vị nằm ở phía bên phải so với đường thẳng t.

Còn các cặp góc chẳng hạn như góc P₁ và D₂ , P₂ và D₁ cũng là các cặp góc khác gốc, nằm ở cùng một phía so với đường thẳng t nhưng không phải là các cặp góc đồng vị vì chúng không nằm ở vị trí giống nhau trên hai đường thẳng f và r.

4. Các dạng bài tập thường gặp về góc đồng vị

4.1. Dạng 1: Nhận biết hai góc đồng vị

*Phương pháp giải:

Dựa vào khái niệm góc đồng vị

Ví dụ: Quan sát hình dưới để hoàn thành các câu sau:

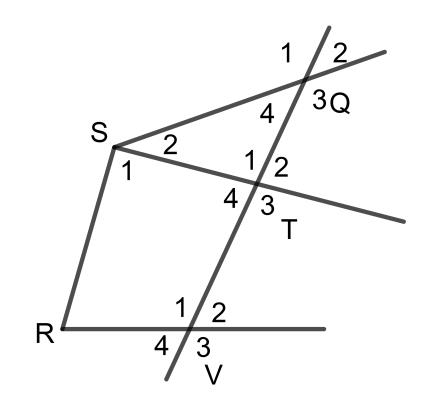
a. và là ......

b. và là ......

c. và .... là cặp góc đồng vị

d. Hai cặp góc đồng vị khác trong hình là: ....

Giải:

a.   và là cặp góc đồng vị

b. và là cặp góc đồng vị

c. và  không phải là cặp góc đồng vị

d. Hai cặp góc đồng vị khác trong hình là: và , và  .

4.2. Dạng 2: Tính số đo của các góc tạo thành từ một đường thẳng cắt hai đường thẳng

*Phương pháp giải:

Áp dụng tính chất về hai góc đồng vị, hai góc kề bù, hai góc đối đỉnh và dựa vào yêu cầu bài toán để phân tích, suy luận tìm ra phương pháp giải thích hợp nhất

Ví dụ: Cho hình sau:

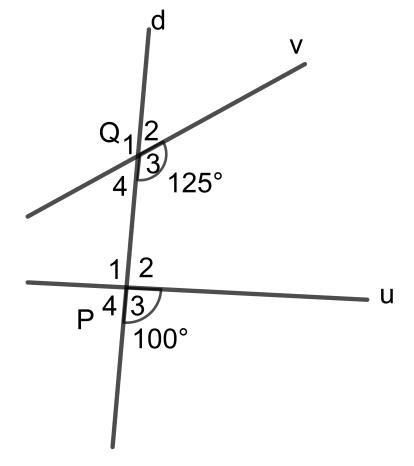
Biết số đo của = 125^o, = 100^o. Tính số đo các góc còn lại trong hình.

Giải:

Ta có: +  = 180^o (hai góc kề bù)

Mà  = 125^o nên    = 180^o -  = 180^o - 125^o = 55^o 

Mặt khác, ta có:    =  (hai góc đối đỉnh)

mà   = 55^o nên   = 55^o

  =  (hai góc đối đỉnh)

mà   = 125^o nên   = 125^o 

Tương tự,

Ta có: +  = 180^o (hai góc kề bù)

Mà  = 100^o nên    = 180^o -  = 180^o - 100^o = 80^o 

Mặt khác, ta có:    =  (hai góc đối đỉnh)

mà   = 100^o nên  = 100^o

  =  (hai góc đối đỉnh)

mà   = 80^o nên   = 80^o 

4.3. Dạng 3: Bài tập có kiến thức tổng hợp liên quan đến hai góc đồng vị

*Phương pháp giải:

Tùy vào yêu cầu của bài toán để phân tích, suy luận đưa ra phương pháp giải chính xác và thích hợp nhất.

5. Một số bài tập vận dụng về góc đồng vị

Bài 1: Hãy cho biết các phát biểu sau đúng hay sai.

a. Hai góc có tổng số đo bằng 180^o là hai góc đồng vị

b. Một đường thẳng y cắt hai đường thẳng e và f thì sẽ tạo ra bốn cặp góc đồng vị

c. Nếu một đường thẳng cắt hai đường thẳng mà trong các góc tạo thành có một cặp góc đồng vị bằng nhau thì các cặp góc đồng vị khác cũng bằng nhau

Bài 2: Hãy kể tên một số hình ảnh trong thực tế mà em nhìn thấy về góc đồng vị?

Bài 3: Cho hình vẽ sau:

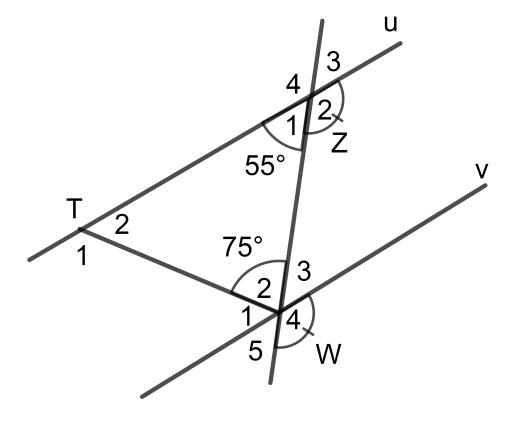
Biết = và số đo của = 55^o, = 75^o. Hãy tính số đo của các góc còn lại trong hình trên.

Trên đây là toàn bộ kiến thức trọng tâm về khái niệm góc đồng vị, cách chứng minh 2 góc đồng vị cùng các dạng bài tập có liên quan với phương pháp giải, ví dụ cụ thể. Bên cạnh đó còn đưa ra một số bài tập vận dụng có lời giải chi tiết. Hy vọng nhũng kiến thức được cung cấp trong bài viết trên sẽ giúp cho các bạn học sinh nắm vững hơn kiến thức, áp dụng thành công vào việc giải các bài tập về chủ đề này.

Chịu trách nhiệm nội dung: GV Nguyễn Thị Trang