Nhận biết số thập phân hữu hạn và giải nhanh một số bài tập thường gặp

Ở chương trình Toán lớp 6 trước, chúng ta đã được tìm hiểu về số thập phân. Vậy tại chương trình Toán lớp 7 nay, chúng ta sẽ được tìm hiểu sâu hơn về số thập phân. Bài viết này sẽ giúp chúng ta tìm hiểu về một trong các dạng số thập phân, cụ thể đó là số thập phân hữu hạn.

I. Số thập phân hữu hạn là gì?

Khái niệm số thập phân hữu hạn: Nếu một phân số tối giản với mẫu dương mà mẫu không có ước nguyên tố khác 2 và 5 thì phân số đó viết được dưới dạng số thập phân hữu hạn.

Ví dụ. Phân số

Khi đó các số 0,2; 0,25; 0,1; .... được gọi là số thập phân hữu hạn.

Nhận xét. Qua ví dụ trên, chúng ta thấy mỗi số hữu tỉ đều được biểu diễn bởi một số thập phân hữu hạn và ngược lại, mỗi số thập phân hữu hạn cũng được biểu diễn một số hữu tỉ.

II. Làm thể nào để biết một phân số viết được dưới dạng số thập phân hữu hạn?

Để nhận biết được một phân số có thể viết được dưới dạng số thập phân hữu hạn hay không, ta thực hiện theo các bước sau:

• Bước 1: Đầu tiên, nếu phân số đã cho chưa tối giản (hoặc phân số có mẫu âm) ta cần viết phân số đã cho dưới dạng phân số tối giản với mẫu số dương.
• Bước 2: Phân tích mẫu số của các phân số đó thành thừa số nguyên tố.
• Bước 3: Quan sát mẫu số của phân số sau khi phân tích, nếu mẫu số không có ước nguyên tố khác 2 và 5 (nghĩa là mẫu số chỉ có ước nguyên tố 2 và 5 ngoài ra không còn ước nào khác) thì kết luận phân số đó viết được dưới dạng số thập phân hữu hạn.

III. Các dạng bài tập liên quan đến số thập phân hữu hạn

1. Dạng 1: Nhận biết các phân số có thể viết được dưới dạng số thập phân hữu hạn

Phương pháp giải.

Áp dụng cách nhận biết một phân số viết được dưới dạng số thập phân hữu hạn đã nêu ở mục II.

Ví dụ 1. Trong các phân số sau đây, phân số nào viết được dưới dạng số thập phân hữu hạn?

Giải.

Đầu tiên, ta cần viết các phân số chưa tối giản về phân số tối giản:

 Ta có 

Phân tích các mẫu số ra thừa số nguyên tố:

 8 = 2³;   6 = 2.3;  5

Nhận xét ước nguyên tố của các mẫu số đó và đưa ra kết luận:

 Ta thấy:

Mẫu số 8 chỉ có ước nguyên tố là 2 nên phân số viết được dưới dạng số thập phân hữu hạn.

Mẫu số 6 có ước nguyên tố khác 2 và 5 nên phân số không viết được dưới dạng số thập phân hữu hạn.

Mẫu số 5 chỉ có ước nguyên tố là 5 nên phân số hay viết được dưới dạng số thập phân hữu hạn.

2. Dạng 2: Viết các phân số đã cho thành số thập phân hữu hạn

Phương pháp giải.

Để viết các phân số đã cho thành số thập phân hữu hạn ta có thể làm theo hai cách sau:

- Cách 1: Thực hiện phép tính chia lấy tử số chia cho mẫu số, kết quả thu được là số thập phân.

- Cách 2: Viết các phân số đã cho thành phân số thập phân (phân số có mẫu là 10, 100, 1000, …). Sau đó viết các phân số thập phân thành số thập phân.

Ví dụ 2. Hãy viết các phân số sau đây thành số thập phân hữu hạn: .

Giải.

Cách 1. Ta thực hiện phép tính chia tử cho mẫu:

Vậy .

Vậy .

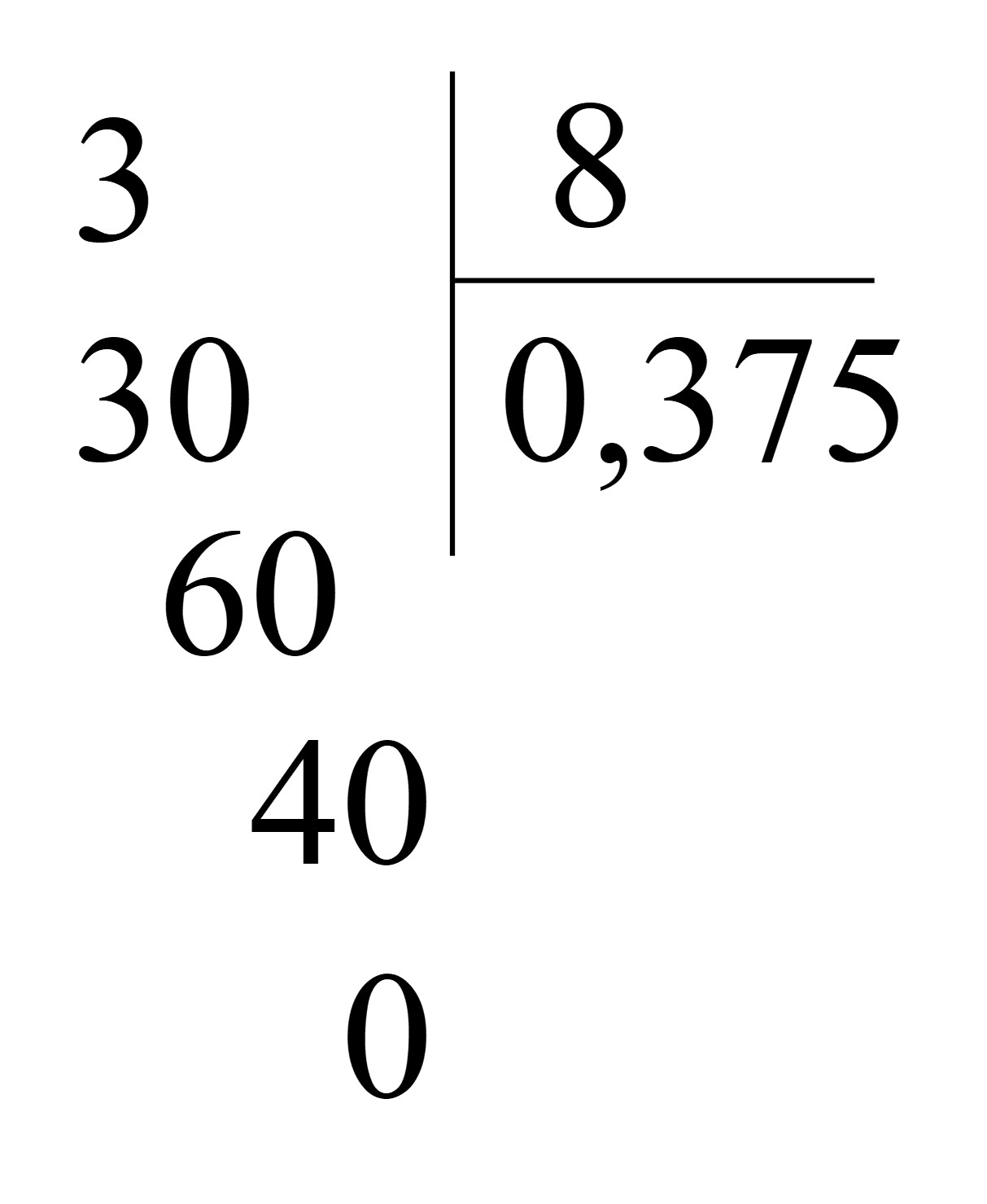
Vậy .

Cách 2. Viết các phân số đã cho thành phân số thập phân:

Ta có:

3. Dạng 3: Viết các số thập phân hữu hạn thành phân số

Phương pháp giải.

Viết các số thập phân hữu hạn thành phân số, đầu tiên ta viết các số thập phân hữu hạn đã cho thành phân số thập phân. Sau đó chúng ta rút gọn các phân số thập phân đó.

Ví dụ 3. Chuyển các số sau thành phân số tối giản:

Giải.

Ta có:

4. Dạng 4: Thực hiện các phép tính liên quan đến số thập phân hữu hạn, bài toán tìm x và tính giá trị biểu thức

Phương pháp giải.

Thực hiện các phép tính cộng, trừ, nhân, chia số thập phân như đã học ở chương trình Toán lớp 6.

Ví dụ 4. Tính giá trị của các biểu thức sau:

a) 14,5 + 25,6 + 25,5

b) 48,02 - (11 - 2,98)

Giải.

a) 14,5 + 25,6 + 25,5

= 14,5 +25,5 +25,6

= 40 + 25,6

= 65,6

b) 48,02 - (11 - 2,98)

= 48,02 - 11 + 2,98

= 48,02 + 2,98 -11

= 51 -11

= 40

Ví dụ 5. Tìm x, biết:

a) x + 2,05 = 45,6

b) 2x - 0,8 = 12,04

Giải.

a) x + 2,05 = 45,6

x= 45,6-2,05                            

x= 43,55

b) 2x - 0,8 = 12,04

2x =12,04 +0,8                      

2x =12,84

x= 12,84 : 2

x= 6,42

IV. Các bài tập vận dụng về số thập phân hữu hạn

Bài 1. Phát biểu nào sau đây là đúng?

A. Một phân số tối giản với mẫu dương có thể viết được dưới dạng số thập phân hữu hạn khi mẫu có ước nguyên tố khác 2 và 5.

B. Một phân số tối giản với mẫu dương có thể viết được dưới dạng số thập phân hữu hạn khi mẫu chỉ có ước nguyên tố của 2.

C. Một phân số tối giản với mẫu dương có thể viết được dưới dạng số thập phân hữu hạn khi mẫu không có ước nguyên tố khác 2 và 5.

D. Một phân số tối giản với mẫu dương có thể viết được dưới dạng số thập phân hữu hạn khi mẫu chỉ có ước nguyên tố của 5.

Bài 2. Chọn câu trả lời đúng. Phân số có thể viết thành số thập phân hữu hạn là:

A.

B.

C.

D.

Bài 3. Chọn câu trả lời đúng. Phân số không viết được dưới dạng số thập phân hữu hạn là:

A.

B.

C.

D.

Bài 4. Trong các phân số sau đây, phân số nào có thể viết được dưới dạng số thập phân hữu hạn:

Hãy chuyển các phân số đó thành số thập phân hữu hạn.

Bài 5. Tính giá trị của các biểu thức sau, biết x = 2,5; y= 5,6.

a) A= (x + 4,5) - (y+4,4)

b) B = 2x - 5y + 10

Bài viết đã tổng hợp các kiến thức liên quan đến số thập phân hữu hạn và phương pháp giải một số bài tập thường gặp. Mong rằng qua bài viết này các bạn sẽ nắm vững kiến thức về số thập phân hữu hạn và có thể áp dụng vào giải các bài tập một cách chính xác nhất.

Chịu trách nhiệm nội dung: GV Nguyễn Thị Trang