Bình phương là gì? Các tính chất của bình phương

Bình phương là khái niệm mới mà lên lớp 6 các bạn mới được nghe đến và được học. Vậy bình phương của một số tự nhiên là gì? Làm thế nào để chúng ta biết cách đọc tên và giải các bài tập liên quan đến bình phương? Bài viết dưới đây sẽ giúp các bạn giải quyết những thắc mắc đó.

1. Bình phương là gì?

Bình phương (hay còn gọi là mũ hai) là tích của số đó với chính nó.

Kí hiệu: x.x = x²

Trong đó x được gọi là cơ số

Cách đọc: x² có thể đọc là “bình phương của x” , “ x bình phương” hoặc “ x mũ hai ”

Ví dụ:

+ 5² đọc là bình phương của 5, 5 bình phương hoặc 5 mũ hai

+ 6² Bình phương của 6, 6 bình phương hoặc 6 mũ hai là: 6²

2. Tính chất bình phương của một số

+ Bình phương của 1 số luôn lớn hơn hoặc bằng 0

+ Bình phương của 1 số nguyên được gọi là số chính phương

* Ở chương này, chúng ta học về số tự nhiên, vì vậy bình phương của một số tự nhiên cũng là số chính phương. Các tính chất của số chính phương sẽ đúng với tính chất bình phương của một số tự nhiên.

Nhắc lại một số tính chất của số chính phương:

+ Các số chính phương sẽ tận cùng là: 0; 1; 4; 5; 6; 9. Những số có tận cùng là: 2; 3; 7; 8 sẽ không thể là số chính phương.

+ Khi phân tích ra thừa số nguyên tố, số chính phương chỉ chứa các thừa số nguyên tố với số mũ chẵn.

3. Cách tính bình phương của một số

Để tính bình phương của một số, ta lấy số đó nhân với chính nó.

Ví dụ: Tính bình phương của 5

5² = 5.5 = 25

11² = 11.11 = 121

Số 25 và số 121 còn được gọi là số chính phương

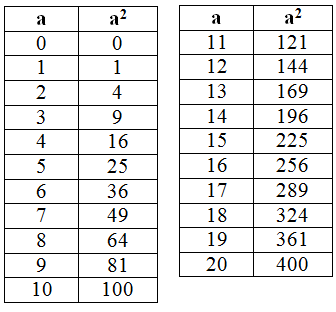
4. Bảng bình phương của các số tự nhiên

Dưới đây là bảng bình phương của các số tự nhiên thường gặp từ 1 đến 20

5. Các dạng bài tập cơ bản về số bình phương

5.1. Dạng 1: Đọc tên và nhận biết số bình phương

*Phương pháp giải:

+ Dựa vào bảng bình phương của 20 số tự nhiên đầu tiên.

+ Dựa vào khái niệm của số bình phương.

+ Dựa vào các cách đọc tên để đọc được tên của số bình phương.

Ví dụ 1:

Đọc tên các số 13² bằng các cách có thể

Giải

Ta có ba cách đọc tên:

+ 13 bình phương

+ Bình phương của 13

+ 13 mũ hai

Ví dụ 2: Trong các số sau, số nào là số bình phương: 15, 25, 36, 42

Giải

Dựa vào bảng số bình phương của các số tự nhiên từ 1 đến 20 để giải bài toán

Từ bảng ta thấy

+ số 25 là bình phương của 5

+ số 36 là bình phương của 6

Bài tập luyện tập

Bài 1: Đọc tên các số sau bằng các cách có thể: 4², 9², 15²

Bài 2: Viết các số sau theo tên gọi đúng:

1. 3 bình phương
2. Bình phương của 8
3. 16 mũ hai
4. Bình phương của 7

Bài 3: Trong các số sau, số nào là bình phương của một số: 85, 100, 125, 225, 400

Bài 4: Viết các số sau thành bình phương của các số tự nhiên: 81, 144, 196, 289

5.2. Dạng 2: Tính giá trị bình phương của 1 số

*Phương pháp giải:

Dựa vào khái niệm và cách tính bình phương của một số để giải bài toán

Ví dụ: Tính giá trị bình phương của 6², 13², 8²

Giải

Ta có

6² = 6.6 = 36

13² = 13.13 = 169

8² = 8.8 = 64

Bài tập luyện tập

Bài 1: Tính giá trị bình phương của 2², 7², 10², 11², 14²

Bài 2: Viết các tích sau bằng cách dùng bình phương của một số tự nhiên.

1. 19.19

2. 25.25

3. 27.27

4. 65.65

Bài 3: Tìm các số tự nhiên từ 100 đến 300 là bình phương của một số tự nhiên

5.3. Dạng 3: Bài tập chứng minh liên quan đến bình phương của một số tự nhiên

*Phương pháp giải:

Những bài toán này không có cách làm cụ thể vì vậy chúng ta sẽ áp dụng khái niệm và dựa vào yêu cầu của từng bài để phân tích và đưa ra cách giải

Bài 1: Chứng minh rằng tổng của các bình phương 2 số tự nhiên liên tiếp là một số lớn hơn 1

Bài 2: Chứng minh rằng hiệu của các bình phương 2 số tự nhiên kém nhau 2 đơn vị là một số chia hết cho 4.

Hi vọng bài viết này sẽ giúp các bạn học sinh hiểu về bình phương của một số tự nhiên và biết cách đọc tên cũng như biết các dạng bài tập liên quan đến bình phương.

Chịu trách nhiệm nội dung: GV Nguyễn Thị Trang