Hình nón tròn xoay và các công thức cần ghi nhớ

Trong chương trình bậc THPT, khái niệm về hình nón tròn xoay là một khái niệm hoàn toàn mới. Ở kiến thức lớp 9 các dạng toán thực tế thông thường chỉ nhắc đến phần công thức và hoàn toàn không tường minh như cách diễn đạt của chương trình toán 12 về hình nón tròn xoay. Ở chủ đề này chúng ta sẽ được tìm hiểu thế nào là hình nón tròn xoay và các dạng toán có liên quan.

1. Định nghĩa hình nón tròn xoay (khối nón tròn xoay)

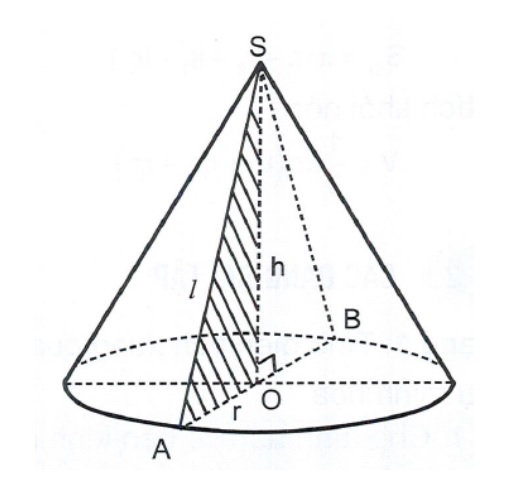
Cho tam giác SOA vuông tại O. Quay tam giác đó quanh cạnh góc vuông SO tạo ra hình nón tròn xoay.

Khối nón là phần không gian giới hạn bởi một hình nón tròn xoay, kể cả hình nón đó.

Các thông số thường gặp:

• r = OA = OB : bán kính đáy.

• h = SO : chiều cao của hình nón.

• I = SA : đường sinh của hình nón.

• Góc ASB : góc ở đỉnh.

2. Các công thức hình nón tròn xoay

Diện tích xung quanh (S_xq ) của hình nón tròn xoay

S_xq = π.r.l

Trong đó

• r là bán kính đáy hình nón

• l : đường sinh hình nón

• S_xq là diện tích xung quanh

Diện tích xung quanh của hình nón tròn xoay cũng là diện tích xung quanh của khối nón tròn xoay.

Diện tích đáy (S_đ ) của hình nón tròn xoay

S_đ = πr²

Trong đó

•  r là bán kính đáy hình nón

Diện tích toàn phần (S_tp) hình nón tròn xoay

Diện tích toàn phần của hình nón tròn xoay = Diện tích xung quanh + Diện tích đáy (của hình nón được cho)

S_tp = S_xq + S_đ

• S_tp là diện tích toàn phần

• S_xq là diện tích xung quanh

• S_đ là diện tích đáy

Thể tích của khối nón tròn xoay

Khi có chiều cao là h và có diện tích đáy thì thể tích của khối nón tròn xoay là

V = .S_đ .h = .π r².h 

Trong đó

• V là thể tích 

• h là chiều cao

• r là bán kính

• S_đ là diện tích đáy 

3. Bài tập về hình nón tròn xoay

3.1. Tính diện tích xung quanh, diện tích toàn phần của hình nón tròn xoay

Bài 1: Cho hình nón có bán kính đáy là 10, chiều cao là 12. Diện tích xung quanh hình nón là:

A. π

B. π

C.

D.

Bài 2: Cho ΔABC vuông tại C, = 60^o, AB = 2a, quay ΔABC quanh trục AC ta được hình nón có diện tích xung quanh bằng:

A. πa²

B. πa²

C.  a²

D. a²

3.2. Thiết diện của mặt phẳng về phần không gian bên trong hình nón tròn xoay

Bài 3: Cắt một hình nón bằng một mặt phẳng qua trục được thiết diện là tam giác vuông cân có cạnh góc vuông bằng a. Khi đó diện tích xung quanh của hình nón bằng:

A.  a²

B.  π.a²

C. 5 π.a²

D. 10 π.a²

Bài 4: Cho hình nón tròn xoay có đường cao h = 8a, r = 6a, mặt phẳng (P) đi qua đỉnh của hình nón và cắt mặt đáy với dây cung có độ dài là 4a, thiết diện hình tạo thành là tam giác cân tại đỉnh của hình nón. Tính diện tích S của thiết diện được tạo ra

A. S = a²

B. S = a²

C. S = a²

D. S =

Bài 5: Cho hình nón đỉnh S, đường cao SO. Gọi A và B là hai điểm thuộc đường tròn đáy của hình nón sao cho khoảng cách từ O đến AB bằng 2 và = 30^o; = 60^o. Tính diện tích xung quanh hình nón.

A.

B.

C.

D.

Chúng ta cần đặc biệt lưu ý về các dạng toán có liên quan đến hình nón tròn xoay, đây là các bài toán thường xuyên xuất hiện trong các đề thi trung học phổ thông quốc gia và các đề thi thử ở các trường trên toàn quốc. Mức độ dao động từ nhận biết đến thông hiểu, thậm chí có năm mức độ vận dụng có sự xuất hiện của hình nón tròn xoay kết hợp với một chút kiến thức về cực trị. Áp dụng kiến thức về hình nón tròn xoay vào giải quyết một số bài toán thực tế có liên quan đến thể tích, diện tích bề mặt cũng là một trong số các dạng toán cần được chú trọng.

Chịu trách nhiệm nội dung: GV Nguyễn Thị Trang