Table of Contents
Khối nón về bản chất nó tương đồng với khối chóp, tuy nhiên ở khối chóp đáy là đa giác còn ở khối nón đáy là một hình tròn. Trong chương trình bậc THPT, toán 12 mang định nghĩa một cách chi tiết về khối nón. Ở thực tế ta có thể sử dụng hình ảnh chiếc nón lá để minh họa cho khối nón, nhờ hình ảnh trực quan sinh động, học sinh sẽ dễ dàng tiếp cận với chủ đề hơn.
1. Khối nón là gì?
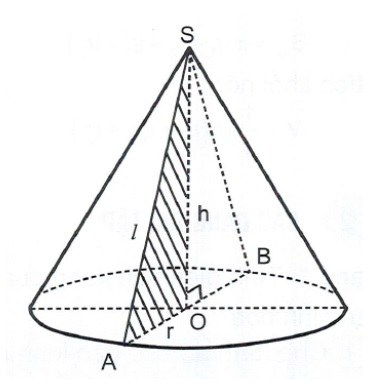
Cho tam giác SOA vuông tại O. Quay tam giác đó quanh cạnh góc vuông SO tạo ra hình nón tròn xoay.
Khối nón là phần không gian giới hạn bởi một hình nón tròn xoay, kể cả hình nón đó.
Các thông số thường gặp:
• r = OA = OB : bán kính đáy
• h = SO : chiều cao của hình nón
• I = SA : đường sinh của hình nón
• Góc ASB: góc ở đỉnh
Có 3 loại hình nón:
- Hình nón cụt
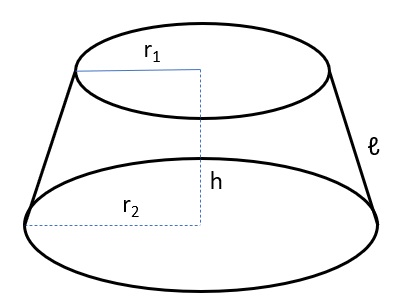
- Hình nón tròn xoay

- Hình nón xiên
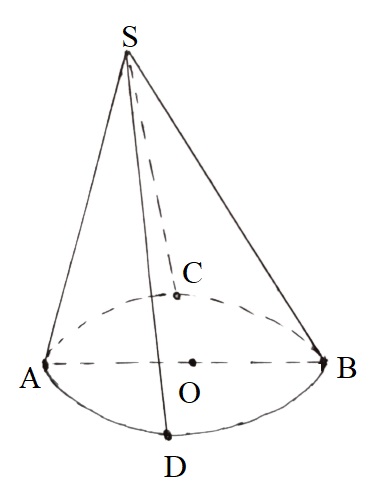
2. Công thức thể tích khối nón
Thể tích khối nón được tính bởi công thức:
V =
Trong đó
• V là thể tích hình nón
• r là bán kính của hình nón
• h là đường cao (hay còn gọi là chiều cao) của hình nón
3. Diện tích xung quanh hình nón (khối nón)
Sxq = π.r.l
4. Thể tích khối nón tròn xoay
Thể tích khối nón tròn xoay có công thức tính là
V =
5. Thể tích khối nón cụt
V =
6. Bài tập về khối nón
Bài 1: Cho hình nón có góc ở đỉnh 1200 diện tích xung quanh bằng 36πa2. Tính thể tích V của khối nón đã cho.
A.
B.
C. 3 πa3
D.
ĐÁP ÁN
∗ Phương pháp
Sử dụng giả thiết ta lập được một hệ phương trình cho bán kính đáy và độ dài đường sinh. Áp dụng định lý Py-ta-go để tìm được độ dài đường cao của hình nón. Áp dụng công thức thể tích để tìm thể tích của khối nón.
∗ Cách giải
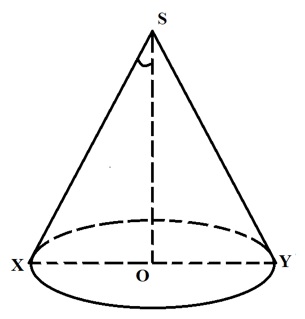
Gọi r, l lần lượt là bán kính đáy và độ dài đường sinh của nón. Do đó XO = r và SX = l
Khi đó theo công thức diện tích xung quanh ta có
Sxq = π.r.l
Mặt khác Sxq = 36πa2
Do đó rl = 36a2 (1)
Hạ đường cao SO xuống đáy.
Khi đó theo giả thiết ta có góc XSO = 60o
Trong tam giác vuông SXO ta có
sin
⇒ sin 60o =
⇒ r =
Từ (1) và (2) ta có
⇔
Áp dụng định lý Py-ta-go trong tam giác vuông IAO ta nhận được
SO2 = SX2 - XO2
= l2 - r2
=
=
⇒ SO =
Thể tích khối nón là
V =
=
=
→ Chọn câu D.
Bài 2: Cắt một hình nón bằng một mặt phẳng đi qua trục của nó ta được thiết diện là một tam giác vuông cân có cạnh huyền bằng 5a, thể tích của khối nón đó là:
A.
B.
C.
D.
ĐÁP ÁN
∗ Phương pháp
Thể tích của hình nón: V =
Trong đó: R:bán kính đáy, l: độ dài đường sinh
∗ Cách giải
Tam giác ABC vuông cân tại A, AH ⊥ BC
⇒ AH = HB = HC =
AB = AH
Ta có h2 = l2 - R2 nên suy ra
h =
=
Thể tích của hình nón:
V =
=
=
→ Chọn câu A.
Bài 3: Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 4a, tam giác SAB đều. Thể tích của hình nón đỉnh S đáy là đường tròn nội tiếp ABCD là:
A.
B.
C.
D.
ĐÁP ÁN
∗ Cách giải
Hình nón đỉnh S đáy là đường tròn nội tiếp ABCD có chiều cao bằng chiều cao của hình chóp h = SO
Bán kính đáy là bán kính đường tròn nội tiếp ABCD: r = 2a và đường sinh là l = SM với M là trung điểm AB.
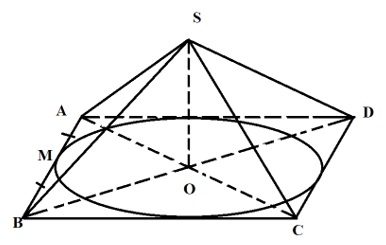
Tam giác SAB đều nên SA = AB = 4a.
Xét tam giác SAO vuông tại O, ta có:
h = SO =
=
=
Bán kính đáy của hình nón là:
R = OM = 2a
Vậy thể tích của hình nón đỉnh S đáy là đường tròn ngoại tiếp ABCD là:
V =
=
=
→ Chọn câu A.
Bài 4: Cho hình nón (N) có thiết diện qua trục là tam giác vuông cân có diện tích bằng 9. Khối nón sinh bởi (N) có thể tích bằng
A. 6π
B. 3π
C. 9π
D. π
ĐÁP ÁN
∗ Cách giải

Giả sử thiết diện là tam giác vuông cân SAB. Gọi bán kính của hình nón (N) là r.
Do SΔSAB = 9
⇔
⇒ r = 3
Vậy thể tích sinh bởi (N):
V =
=
= 9π
→ Chọn câu C.
Bài 5: Cho hình chóp tam giác đều cạnh đáy bằng 5, cạnh bên hình chóp tạo với đáy một góc bằng 300. Chiều cao và bán kính đáy của khối nón nội tiếp chóp tam giác đều đó.
A. r =
B. r =
C. r =
D. r =
ĐÁP ÁN
∗ Cách giải
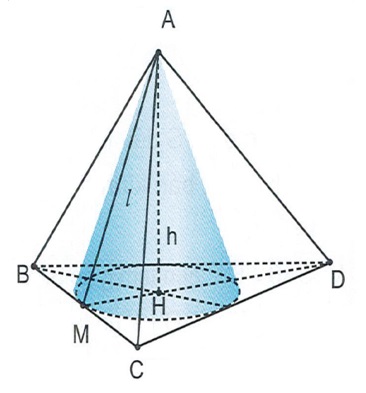
Gọi H là trọng tâm tam giác đều BCD.
Ta có: AH ⊥ (BCD)
Hình nón đỉnh A đáy là đường tròn nội tiếp BCD có chiều cao bằng chiều cao của hình chóp h = AH
Bán kính đáy là bán kính đường tròn nội tiếp BCD: r = HM (M là trung điểm BC) và đường sinh l = AM.
Vì tam giác BCD đều cạnh a nên DM =
Do H là tâm tam giác BCD nên:
MH =
=
=
Vì cạnh bên tạo với đáy một góc bằng 300 nên
AH = HD . tan30o
=
=
Do đó
r =
→ Chọn câu C.
Trong chủ đề này, ngoại trừ lý thuyết đi chi tiết về các định nghĩa liên quan đến khối chóp thì ở phần bài tập phân dạng rất rõ ràng. Từ dạng nhận biết là tính thể tích khối nón cho đến dạng bài tập thông hiểu là xác định mô tả thiết diện của khối nón phù hợp với nội dung bài, còn ở mức độ vận dụng các dạng bài tập nâng cao hơn của thiết diện và xây dựng khối nón thỏa tình chất ngoại tiếp hoặc nội tiếp khối đa diện trong đề. Đặc biệt ta cần lưu ý các phương pháp giải để có thể tiếp cận các dạng bài tập một cách chủ động hơn.
Chịu trách nhiệm nội dung: GV Nguyễn Thị Trang
